题目内容
【题目】已知正方形ABCD的边长为2,正方形内有一动点P,求点P到三个顶点A、B、C的距离之和的最小值( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
画出图形即可;将△ABP沿点B逆时针旋转60°到△A1BP1,过A1作A1H⊥BC,交CB的延长线于H,连接P1P,由旋转的性质及两点之间线段最短即可得出结论;
将△ABP沿点B逆时针旋转60°到△A1BP1,
如图过A1作A1H⊥BC,交CB的延长线于H,连接P1P,
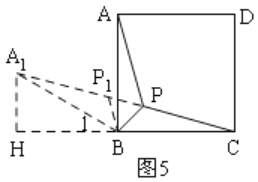
易得:A1B=AB,PB=P1B,PA=P1A1,∠P1BP=∠A1BA=60°,
∵PB=P1B,∠P1BP=60°,
∴△P1PB是正三角形,
∴PP1=PB,
∴PA+PB+PC=P1A1+PP1+PC,
∴当A1、P1、P、C四点共线时PA+PB+PC最小,最小值是A1C的长度
此时∠A1BA=∠P1BP=60°,∠CBA=90°,
∴∠1=30°,
在Rt△A1HB中,A1B=AB=2,∠1=30°,得:A1H=1,BH=![]() ,
,
∴CH=![]() +2
+2
在Rt△A1HC中,由勾股定理得:
![]() ,
,
∴点P到三个顶点A、B、C的距离之和的最小值![]()
故选C

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】新个税法于2018年1月1日起施行,2018年10月1日起施行最新“起征点:5000元”和税率,《中华共和国个人所得税》中的个人所得税税率如下:
级数 | 全月应纳税所得额 | 税率(%) |
1 | 不超过3000元的部分 | 3 |
2 | 超过3000元至12000元的部分 | 10 |
3 | 超过12000元至25000元的部分 | 20 |
其中“全月应纳税所得额”是指从工资、薪金收入中减去5000元后的金额。(本题只讨论上表内容)
(1)若某一月份扣除税后拿了8000,他交了多少税?
(2)若某一月份纳税额为m元(m>0),他的税前收入是多少?