题目内容
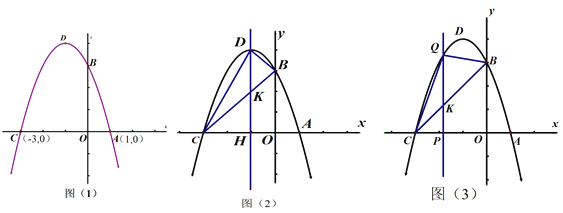
【题目】已知,如图,抛物线与x轴交点坐标为A(1,0),C(-3,0),
(1)若已知顶点坐标D为(-1,4)或B点(0,3),选择适当方式求抛物线的解析式.
(2)若直线DH为抛物线的对称轴,在(1)的基础上,求线段DK的长度,并求△DBC的面积.
(3)将图(2)中的对称轴向左移动,交x轴于点p(m,0)(-3<m<-1),与线段BC、抛物线的交点分别为点K、Q,用含m的代数式表示QK的长度,并求出当m为何值时,△BCQ的面积最大?
【答案】(1)y=-x2-2x+3;(2)3; (3)m=-![]() 时,面积最大.
时,面积最大.
【解析】试题分析:(1)用待定系数法求函数关系式即可;
(2)先根据![]() 得KH=2,所以DK=2,S△DBC=
得KH=2,所以DK=2,S△DBC=![]() DK×OC即可;
DK×OC即可;
(3)先根据QK=QK-KP求出QK=-m2-3m,再由S△BCQ=![]() QK×|OC|得出结果即可.
QK×|OC|得出结果即可.
试题解析:(1)设二次函数解析式为y=a(x+1)2+4
将B(0,3)代入,得a=-1,
∴二次函数解析式为y=-x2-2x+3;
(2)易得DH∥OB,
∴KH:OB=CH:CO
∵C(-3,0),B(0,3)且直线DH是抛物线的对称轴,
∴CH=2,CO=3,OB=3
∴CH=2
∵D(-1,4)
∴DH=4,
∴DK=DH-KH=4-2=2;
∴S△DBC=![]() DK×OC=
DK×OC=![]() ×2×3=3
×2×3=3
(3)QK=QK-KP=-m2-2m+3-(m+3)=-m2-3m.
S△BCQ=![]() QK×|OC|=
QK×|OC|=![]() (-m2-3m)×3=--
(-m2-3m)×3=-- ![]() .
.
∴当m=![]() =-
=-![]() 时,面积最大.
时,面积最大.

练习册系列答案
相关题目