Question

【题目】如图，四边形ABCD是边长为1的正方形，点E在AD边上运动，且不与点A和点D重合，连结CE，过点C作CF⊥CE交AB的延长线于点F，EF交BC于点G．

（1）求证：△CDE≌△CBF；

（2）当DE=时，求CG的长；

（3）连结AG，在点E运动过程中，四边形CEAG能否为平行四边形？若能，求出此时DE的长；若不能，说明理由．

Answer 1

【答案】（1）见解析；（2）；（3）不能.

【解析】

试题分析：（1）先判断出∠CBF=90°，进而判断出∠1=∠3，即可得出结论；

（2）先求出AF，AE，再判断出△GBF∽△EAF，可求出BG，即可得出结论；

（3）假设是平行四边形，先判断出DE=BG，进而判断出△GBF和△ECF是等腰直角三角形，即可得出∠GFB=∠CFE=45°，即可得出结论．

试题解析：（1）如图，在正方形ABCD中，DC=BC，∠D=∠ABC=∠DCB=90°，

∴∠CBF=180°﹣∠ABC=90°，∠1+∠2=∠DCB=90°，

∵CF⊥CE，∴∠ECF=90°，

∴∠3+∠2=∠ECF=90°，∴∠1=∠3，

在△CDE和△CBF中，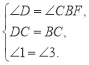

∴△CDE≌△CBF，

（2）在正方形ABCD中，AD∥BC，

∴△GBF∽△EAF，∴，

由（1）知，△CDE≌△CBF，

∴BF=DE=，

∵正方形的边长为1，∴AF=AB+BF=，AE=AD﹣DE=，

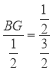∴，，∴BG=，∴CG=BC﹣BG=；

（3）不能，

理由：若四边形CEAG是平行四边形，则必须满足AE∥CG，AE=CG，

∴AD﹣AE=BC﹣CG，

∴DE=BG，

由（1）知，△CDE≌△ECF，

∴DE=BF，CE=CF，

∴△GBF和△ECF是等腰直角三角形，

∴∠GFB=45°，∠CFE=45°，

∴∠CFA=∠GFB+∠CFE=90°，

此时点F与点B重合，点D与点E重合，与题目条件不符，

∴点E在运动过程中，四边形CEAG不能是平行四边形．