题目内容
【题目】如图,在△ABC和△ADE中,点E在BC边上,∠B=∠D,AB=AD,∠BAD=∠CAE,
(1)求证:AE=AC
(2)若∠AEC=60°,将△ADE绕点A逆时针旋转后与△ABC重合,则这个旋转角的度数__
(3)若AC=4,BC=7,∠AEC=60°,求△ABE的面积.

【答案】(1)证明见解析;(2)60° ;(3)3![]()
【解析】
(1)先由∠BAD=∠CAE得出∠BAC=∠DAE,再根据“ASA”证明△ADE≌△ABC,根据全等三角形的对应边相等即可得出AE=AC;
(2)由(1)知AE=AC,结合∠AEC=60°,进而得出△AEC是等边三角形,故可得出旋转角;
(3)首先得出BE的长,再求出△ABE的高,即可得出答案.
(1)证明:∵∠BAD=∠CAE,
∴∠CAE+∠EAB=∠BAD+∠EAB,
即∠CAB=∠EAD,
在△ADE和△ABC中,
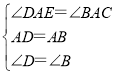 ,
,
∴△ADE≌△ABC(ASA),
∴AE=AC;
(2)由(1)知:AE=AC,
∵∠AEC=60°,
∴△AEC是等边三角形,
∴∠EAC=60°,
∴旋转角的度数为60°;
故答案为:60°;
(2)过点A作AF⊥BC于点F,

由(1)可得:△AEC是等边三角形,
则EC=AC=4,CF=![]()
故BE=BC-EC=7-4=3,AF=![]() ,
,
故△ABE的面积为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目








