Question

【题目】已知函数，其中与成反比例与成正比例，函数的自变量的取值范围是，且当或时，的值均为。

请对该函数及其图象进行如下探究：

（1）解析式探究：根据给定的条件，可以确定出该函数的解析式为： ．

（2）函数图象探宄：①根据解析式，选取适当的自变量，并完成下表：

										．．．
										．．．

②根据表中数据，在如图所示的平面直角坐标系中描点，并画出函数图象．

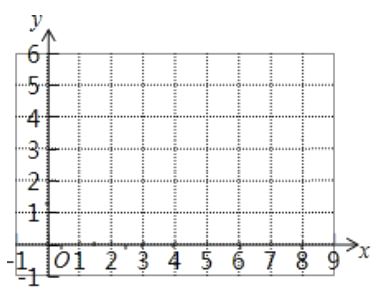
（3）结合画出的函数图象，解决问题：

①当，，时，函数值分别为，则的大小关系为： （用“”或“”表示）

②若直线与该函数图象有两个交点，则的取值范围是 ，此时，的取值范围是 ．

Answer 1

【答案】（1）；（2）见解析；（3）①②，且

【解析】

（1）由题意用待定系数法设设，则有，将已知条件代入得关于k1、k2方程组，即可求得该函数解析式；

（2）①根据题意选取适当数值填表即可；

②在平面直角坐标系中描点，用平滑曲线从左到右顺次连接各点，画出图象；

（3）①由题意结合画出的函数图象运用增减性进行分析即可；

②根据题意观察图象得：x≥，图象最低点为（2，1），依次进行分析即可.

解：（1）设，则有，

由题意得：，解得：，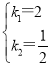

∴该函数解析式为：.

（2）①根据解析式，补全下表：

②根据上表在平面直角坐标系中描点，画出图象：

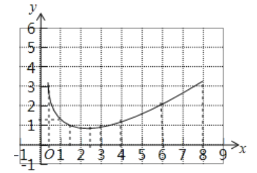
（3）①由（2）中图象可得：（2，1）是图象上最低点，在该点左侧，y随x增大而减小；在该点右侧y随x增大而增大，

∴，

故答案为：，

②观察图象得：x≥，图象最低点为（2，1），

∴当直线y=k与该图象有两个交点时，1＜k≤，

此时x的范围是：且．

故答案为：1＜k≤，且．