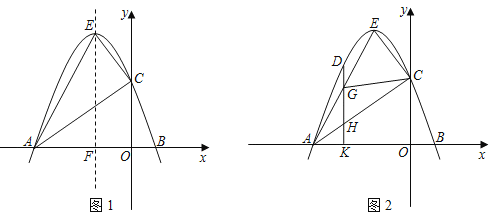ЬтФПФкШн
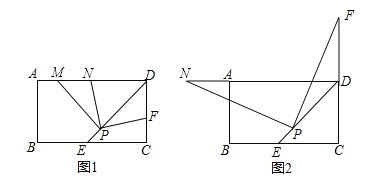
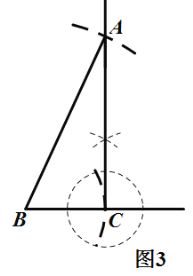
ЁОЬтФПЁПЃЈ1ЃЉШчЭМ1ЃЌдкЁбOжаЃЌABЪЧжБОЖЃЌЯвEFЁЮABЃЌдкжБОЖABЯТЗНЕФАыдВЩЯгавЛИіЖЈЕуHЃЈЕуHВЛгыЕуAЃЌBжиКЯЃЉЃЌЧыНігУЮоПЬЖШЕФжБГпЛГіСгЛЁ![]() ЕФжаЕуPЃЌВЂдкжБЯпABЩЯЛГіЕуGЃЌЪЙжБЯпABЦНЗжЁЯHGPЃЎЃЈБЃСєзїЭМКлМЃЃЌВЛаДзїЗЈЃЉ
ЕФжаЕуPЃЌВЂдкжБЯпABЩЯЛГіЕуGЃЌЪЙжБЯпABЦНЗжЁЯHGPЃЎЃЈБЃСєзїЭМКлМЃЃЌВЛаДзїЗЈЃЉ
 ЁЁЁЁЁЁЁЁ
ЁЁЁЁЁЁЁЁ
ЃЈ2ЃЉГпЙцзїЭМЃКШчЭМ2ЃЌвбжЊЯпЖЮaЁЂcЃЌЧыФугУСНжжВЛЭЌЕФЗНЗЈзїRtЁїABCЃЌЪЙЦфаББпAB=cЃЌвЛЬѕжБНЧБпBC=aЃЎЃЈБЃСєзїЭМКлМЃЃЌВЛаДзїЗЈЃЉ
ЁОД№АИЁПЃЈ1ЃЉШчЭМЫљЪОМћНтЮіЃЛЃЈ2ЃЉШчЭМЫљЪОМћНтЮіЃЎ
ЁОНтЮіЁП
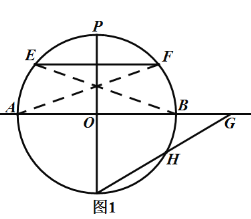
ЃЈ1ЃЉСЌНсAFЁЂBEЃЌзїЙ§AFгыBEЕФНЛЕуКЭдВаФOЕФжБЯпМДПЩЕУГіСгЛЁ![]() ЕФжаЕуPЃЌИУжБЯпгыдВOдкжБЯпABЯТЗННЛгквЛЕуЃЌзїЙ§ИУЕуКЭHЕуЕФжБЯпгыжБЯпABНЛгквЛЕуЃЌМДЮЊЫљЧѓЕФGЕуЃЛ
ЕФжаЕуPЃЌИУжБЯпгыдВOдкжБЯпABЯТЗННЛгквЛЕуЃЌзїЙ§ИУЕуКЭHЕуЕФжБЯпгыжБЯпABНЛгквЛЕуЃЌМДЮЊЫљЧѓЕФGЕуЃЛ
ЃЈ2ЃЉЗНЗЈвЛИљОнжБОЖЫљЖдЕФдВжмНЧЮЊжБНЧЃЌЯШвдABЮЊжБОЖзїдВЃЌдйвдBЮЊдВаФЃЌaЮЊАыОЖзїдВПЩШЗЖЈCЕуЃЌМДПЩЕУRtЁїABCЃЛЗНЗЈЖўРћгУзїДЙЯпЕФЗНЗЈвдCЕуЮЊДЙзузїжБЯп![]() ЃЌдйвдBЮЊдВаФЃЌcЮЊАыОЖзїдВПЩШЗЖЈAЕуЃЌМДПЩЕУRtЁїABCЃЎ
ЃЌдйвдBЮЊдВаФЃЌcЮЊАыОЖзїдВПЩШЗЖЈAЕуЃЌМДПЩЕУRtЁїABCЃЎ
НтЃКЃЈ1ЃЉШчЭМ1ЫљЪОЃЌЕуPЁЂЕуGМДЮЊЫљЧѓЃЛ
ЃЈ2ЃЉЗНЗЈвЛЃК ШчЭМ2ЫљЪОЃЌRtЁїABCМДЮЊЫљЧѓЃЛ
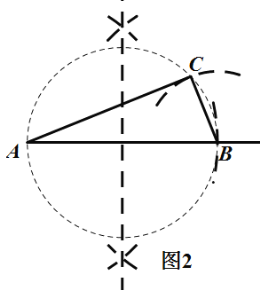
ЗНЗЈЖўЃКШчЭМ3ЫљЪОЃЌRtЁїABCМДЮЊЫљЧѓЃЎ

ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌЦфжа
ЃЌЦфжа![]() гы
гы![]() ГЩЗДБШР§
ГЩЗДБШР§![]() гы
гы![]() ГЩе§БШР§ЃЌКЏЪ§ЕФздБфСП
ГЩе§БШР§ЃЌКЏЪ§ЕФздБфСП![]() ЕФШЁжЕЗЖЮЇЪЧ
ЕФШЁжЕЗЖЮЇЪЧ![]() ЃЌЧвЕБ
ЃЌЧвЕБ![]() Лђ
Лђ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФжЕОљЮЊ
ЕФжЕОљЮЊ![]() ЁЃ
ЁЃ
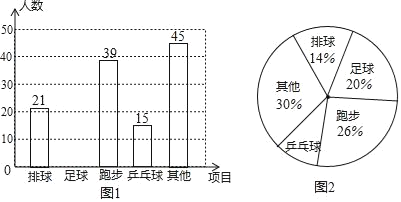
ЧыЖдИУКЏЪ§МАЦфЭМЯѓНјааШчЯТЬНОПЃК
ЃЈ1ЃЉНтЮіЪНЬНОПЃКИљОнИјЖЈЕФЬѕМўЃЌПЩвдШЗЖЈГіИУКЏЪ§ЕФНтЮіЪНЮЊЃК ЃЎ
ЃЈ2ЃЉКЏЪ§ЭМЯѓЬНхГЃКЂйИљОнНтЮіЪНЃЌбЁШЁЪЪЕБЕФздБфСП![]() ЃЌВЂЭъГЩЯТБэЃК
ЃЌВЂЭъГЩЯТБэЃК
|
| ЃЎЃЎЃЎ | ||||||||
| ЃЎЃЎЃЎ |
ЂкИљОнБэжаЪ§ОнЃЌдкШчЭМЫљЪОЕФЦНУцжБНЧзјБъЯЕжаУшЕуЃЌВЂЛГіКЏЪ§ЭМЯѓЃЎ
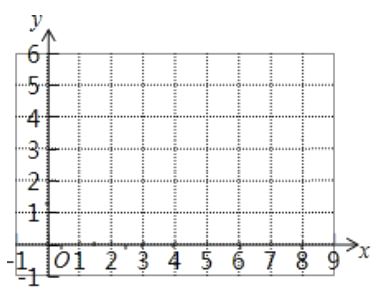
ЃЈ3ЃЉНсКЯЛГіЕФКЏЪ§ЭМЯѓЃЌНтОіЮЪЬтЃК
ЂйЕБ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪБЃЌКЏЪ§жЕЗжБ№ЮЊ
ЪБЃЌКЏЪ§жЕЗжБ№ЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЕФДѓаЁЙиЯЕЮЊЃК ЃЈгУЁА
ЕФДѓаЁЙиЯЕЮЊЃК ЃЈгУЁА![]() ЁБЛђЁА
ЁБЛђЁА![]() ЁББэЪОЃЉ
ЁББэЪОЃЉ
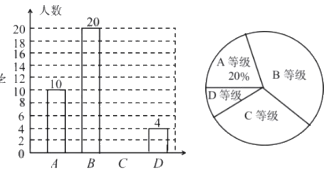
ЂкШєжБЯп![]() гыИУКЏЪ§ЭМЯѓгаСНИіНЛЕуЃЌдђ
гыИУКЏЪ§ЭМЯѓгаСНИіНЛЕуЃЌдђ![]() ЕФШЁжЕЗЖЮЇЪЧ ЃЌДЫЪБЃЌ
ЕФШЁжЕЗЖЮЇЪЧ ЃЌДЫЪБЃЌ![]() ЕФШЁжЕЗЖЮЇЪЧ ЃЎ
ЕФШЁжЕЗЖЮЇЪЧ ЃЎ