��Ŀ����
����Ŀ����1�����ⷢ��
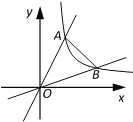
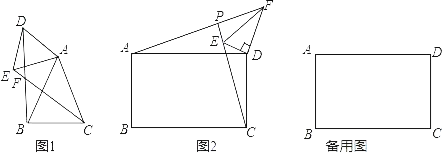
��ͼ1������ABC����ADE�У�AB��AC��AD��AE����BAC����DAE��50��������BD��CE���ڵ�F����գ�
�ٵ�ֵΪ�� �����ڡ�BFC�Ķ���Ϊ�� ����
��2�����̽��
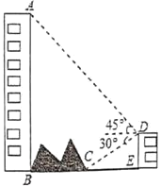
��ͼ2���ھ���ABCD����DEF�У�AD��![]() AB����EDF��90������DEF��60��������AF��CE���ӳ����ڵ�P����
AB����EDF��90������DEF��60��������AF��CE���ӳ����ڵ�P����![]() ��ֵ����APC�Ķ�������˵�����ɣ�
��ֵ����APC�Ķ�������˵�����ɣ�
��3����չ����
�ڣ�2���������£�����DEF�Ƶ�D��ƽ������װ��AF��CE����ֱ�߽��ڵ�P����DF��![]() ��AB��
��AB��![]() ���������P���E�غ�ʱAF�ij���
���������P���E�غ�ʱAF�ij���
���𰸡���1��1��50������2��![]() �����ɼ���������3������P���E�غ�ʱ��AF�ij�Ϊ3��6�����ɼ�����
�����ɼ���������3������P���E�غ�ʱ��AF�ij�Ϊ3��6�����ɼ�����
��������
��1�����ⷢ�֣��ɡ�SAS����֤��DAB�ա�EAC���ɵ�BD��CE����ACE����ABD��������⣻
��2�����̽����ͨ��֤����ADF�ס�CDE���ɵ�![]() ����FAD��DCE��������⣻
����FAD��DCE��������⣻
��3����չ���죺����C��CM��DE���ɹ��ɶ�������CE�ij���������AF�ij���
��1�����ⷢ�֣�
�ߡ�BAC����DAE��50����
���DAB����EAC����AB��AC��AD��AE
���DAB�ա�EAC��SAS��
��BD��CE����ACE����ABD
��![]()
�ߡ�BAC+��ABC+��ACB��180�����ҡ�BFC+��FBC+��FCB����BFC+��ABC+��ABF+��FCB����BFC+��ABC+��ACB��180��
���BFC����BAC��50��
�ʴ�Ϊ1��50��
��2�����̽����
![]() ����APC��90��
����APC��90��
�������£��ߡ�DEF��60������FDE��90��
��DF��![]() DE��
DE��
���ı���ABCD�Ǿ���
��CD��AB����ADC��90��
��AD��![]() DC����ADC����EDF��90��
DC����ADC����EDF��90��
���EDC����ADF����![]()
���ADF�ס�CDE
��![]() ����FAD��DCE
����FAD��DCE
���A����P����D����C�ĵ㹲Բ
���APC����ADC��90��
��3����չ���죺
��ͼ������C��CM��DE����ED�ӳ����ڵ�M��
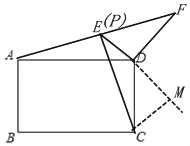
��DF��![]() ����DEF��60������AEC��90��
����DEF��60������AEC��90��
��DE��1����CEM��30��
�ߡ�CEM��30����CM��ED
��![]()
��CD2��CM2+DM2��
��7��![]() +��EM��1��2��
+��EM��1��2��
��CE��2![]()
��![]() ��
��
��AF��6
��ͼ������C��CM��DE����DE�ӳ����ڵ�M��
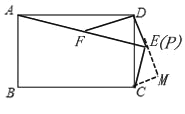
��DF��![]() ����DEF��60������AEC��90��
����DEF��60������AEC��90��
��DE��1����CEM��30��
�ߡ�CEM��30����CM��ED
��![]()
��CD2��CM2+DM2��
��7��![]() +��EM+1��2��
+��EM+1��2��
��CE��![]()
��![]() ��
��
��AF��3
��������������P���E�غ�ʱ��AF�ij�Ϊ3��6��

 ������ҵ��ͬ����ϰ��ϵ�д�
������ҵ��ͬ����ϰ��ϵ�д�����Ŀ����֪����![]() ������
������![]() ��
��![]() �ɷ�����
�ɷ�����![]() ��
��![]() �����������������Ա���
�����������������Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��![]() ���ҵ�
���ҵ�![]() ��
��![]() ʱ��
ʱ��![]() ��ֵ��Ϊ
��ֵ��Ϊ![]() ��
��
��Ըú�������ͼ���������̽����
��1������ʽ̽�������ݸ���������������ȷ�����ú����Ľ���ʽΪ�� ��
��2������ͼ��̽峣��ٸ��ݽ���ʽ��ѡȡ�ʵ����Ա���![]() ��������±���
��������±���
|
| ������ | ||||||||
| ������ |
�ڸ��ݱ������ݣ�����ͼ��ʾ��ƽ��ֱ������ϵ����㣬����������ͼ��
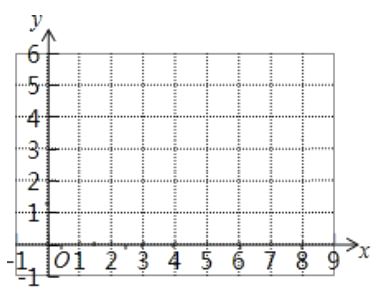
��3����ϻ����ĺ���ͼ������⣺
�ٵ�![]() ��
��![]() ��
��![]() ʱ������ֵ�ֱ�Ϊ
ʱ������ֵ�ֱ�Ϊ![]() ����
����![]() �Ĵ�С��ϵΪ�� ������
�Ĵ�С��ϵΪ�� ������![]() ������
������![]() ����ʾ��
����ʾ��
����ֱ��![]() ��ú���ͼ�����������㣬��
��ú���ͼ�����������㣬��![]() ��ȡֵ��Χ�� ����ʱ��
��ȡֵ��Χ�� ����ʱ��![]() ��ȡֵ��Χ�� ��
��ȡֵ��Χ�� ��