题目内容
【题目】如图,BD是△ABC的角平分线,点E、F分别在边BC、AB上,且DE∥AB,∠DEF=∠A.
(1)求证:BE=AF;
(2)设BD与EF交于点M,联结AE交BD于点N,求证:BNMD=BDND.

【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)先证明四边形ADEF为平行四边形得到AF=DE,再证明∠DBE=∠BDE得到BE=DE,则BE=AF;
(2)如图,根据平行线分线段成比例定理,由EF∥AC得到AF:AB=DM:BD等量代换得DE:AB=DM:BD,再由DE∥AB得到DE:AB=DN:BN,则DM:BD=DN:BN,然后利用比例的性质即可得到结论.
试题解析:
证明:(1)∵DE∥AB,
∴∠A+∠ADE=180°,
∵∠DEF=∠A,
∴∠DEF+∠ADE=180°,
∴EF∥AD,
∴四边形ADEF为平行四边形,
∴AF=DE,
∵BD是△ABC的角平分线,
∴∠DBE=∠ABD,
∵DE∥AB,
∴∠ABD=∠BDE,
∴∠DBE=∠BDE,
∴BE=DE,
∴BE=AF;
(2)如图,
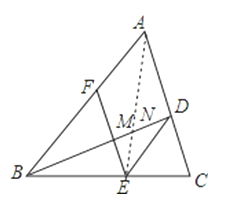
∵EF∥AC,
∴AF:AB=DM:BD,
∵AF=DE,
∴DE:AB=DM:BD,
∵DE∥AB,
∴DE:AB=DN:BN,
∴DM:BD=DN:BN,
即BN·MD=BD·ND.

练习册系列答案
相关题目