题目内容
【题目】抛物线y=ax2+bx﹣3交x轴于B、C两点,且B的坐标为(﹣2,0)直线y=mx+n过点B和抛物线上另一点A(4,3)
(1)求抛物线和直线的解析式;
(2)若点P为抛物线上的一个动点,且在直线AB下方,过P作PQ∥x轴,且PQ=4(点Q在P点右侧).以PQ为一边作矩形PQEF,且点E在直线AB上.求矩形PQEF的最大值.并求出此时点P的坐标;
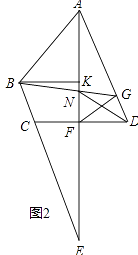
(3)如图2,在(2)的结论下,连接AP、BP,设QE交于x轴于点D,现即将矩形PQEF沿射线DB以每秒1个单位长度的速度平移,当点D到达点B时停止,记平移时间为t,平移后的矩形PQEF为P′Q′E′F′,且Q′E′分别交直线AB、x轴于N、D′,设矩形P′Q′E′F′与△ABP的重叠部分面积为s,当NA= ![]() ND′时,求s的值.
ND′时,求s的值.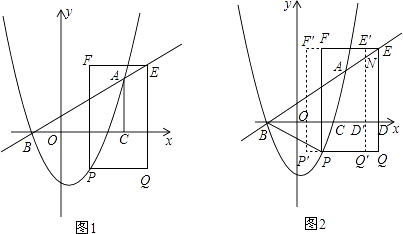
【答案】
(1)
解:∵B的坐标为(﹣2,0)直线y=mx+n过点B和抛物线上另一点A(4,3),
∴ ![]() ,
,
∴ 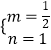 ,
,
∴直线解析式为y= ![]() x+1,
x+1,
∵抛物线过点A,B,
∴ ![]() ,
,
∴ 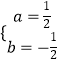 ,
,
∴y= ![]() x2﹣
x2﹣ ![]() x﹣3
x﹣3
(2)
解:由矩形的周长为2(PQ+EQ)=8+2EQ,要使周长最大,EQ最大即可,
设P(a, ![]() a2﹣
a2﹣ ![]() a﹣3),
a﹣3),
∴Q(a+4, ![]() a2﹣
a2﹣ ![]() a﹣3),E(a+4,
a﹣3),E(a+4, ![]() a+3),
a+3),
∴EQ= ![]() a+3﹣(
a+3﹣( ![]() a2﹣
a2﹣ ![]() a﹣3)=﹣
a﹣3)=﹣ ![]() (a﹣1)2+
(a﹣1)2+ ![]() ,
,
∴当a=1时,EQ最大,P(1,﹣3)
(3)
解:如图2,
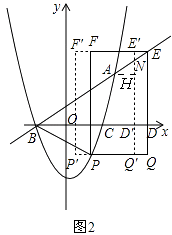
①N在线段AE上时,有DD′=t,oD′=5﹣t,D′(5﹣t,0),N(5﹣t,﹣ ![]() t+
t+ ![]() ),
),
过点A作AH⊥ND′,
∴AH∥x轴,
∴NH=﹣ ![]() t+
t+ ![]() ﹣3=﹣
﹣3=﹣ ![]() t+
t+ ![]() ,
,
∴M(0,1)
∴OM=1,
∴BM= ![]() ,
,
∴sin∠MBO= ![]() ,
,
∵AH∥x轴,
∴∠NAH=∠MBO,
∴sin∠MBO= ![]() ,
,
∴ ![]() ,
,
∴NA= ![]() (﹣
(﹣ ![]() t+
t+ ![]() )
)
由NA= ![]() ND′,
ND′,
∴ ![]() (﹣
(﹣ ![]() t+
t+ ![]() )=
)= ![]() (﹣
(﹣ ![]() t+
t+ ![]() ),
),
∴t= ![]() ,
,
∵BP的解析式为y=﹣x﹣2,
xJ= ![]() ,yJ=﹣
,yJ=﹣ ![]() ,
,
∴J( ![]() ,﹣
,﹣ ![]() ),
),
∵Q( ![]() ,
, ![]() ),
),
∴QJ= ![]() ,
,
同理:IP= ![]() ,
,
∴S=S梯形+S△IDA= ![]() ,
,
②N在AB上时,同①的方法一样,得到MQ=2,NK=1,
S=S梯形MQPI+S梯形PKNI= ![]() ×(2+
×(2+ ![]() )×
)× ![]() +
+ ![]() (1+
(1+ ![]() )×(
)×( ![]() ﹣1)=
﹣1)= ![]()
【解析】(1)用待定系数法求出抛物线和直线的解析式,(2)先确定出要使周长最大,EQ最大即可,求出EQ函数关系式即可;(3)①N在线段AE上时QJ= ![]() ,IP=
,IP= ![]() ,再求出面积S=S梯形+S△IDA , ②N在AB上时,MQ=2,NK=1在计算面积即可S=S梯形MQPI+S梯形PKNI
,再求出面积S=S梯形+S△IDA , ②N在AB上时,MQ=2,NK=1在计算面积即可S=S梯形MQPI+S梯形PKNI
【考点精析】通过灵活运用二次函数的图象和二次函数的性质,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案