题目内容
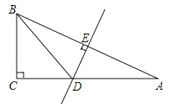
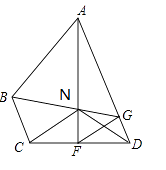
【题目】一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形AOB, 改变△ACD的位置(其中A点位置始终不变),使三角形ACD的一边与三角形AOB的某一边平行时,写出∠BAD的所有可能的值 . 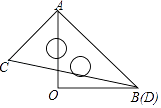
【答案】15°,30°,45°,75°,105°,135°,150°,165°
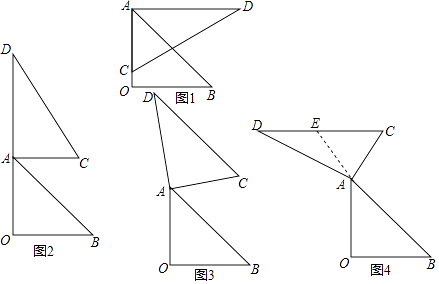
【解析】解:分8种情况讨论: 1)如图1,AD边与OB边平行时,∠BAD=45°;
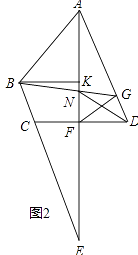
2)如图2,当AC边与OB平行时,∠BAD=90°+45°=135°;
3)如图3,DC边与AB边平行时,∠BAD=60°+90°=150°,
4)如图4,DC边与OB边平行时,∠BAD=135°+30°=165°,
5)如图5,DC边与OB边平行时,∠BAD=45°﹣30°=15°;
6)如图6,DC边与AO边平行时,∠BAD=15°+90°=105°
7)如图7,DC边与AB边平行时,∠BAD=30°,
8)如图8,DC边与AO边平行时,∠BAD=30°+45°=75°
故答案为:15°,30°,45°,75°,105°,135°,150°,165°.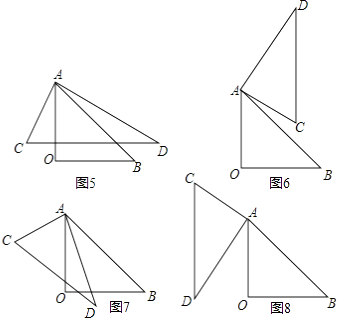
要分类讨论,不要漏掉一种情况,也可实际用三角板操作找到它们之间的关系;再计算.

练习册系列答案
相关题目