Question

【题目】问题背景：

如图①，在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°.E、F分别是BC、CD上的点.且∠EAF＝60°.探究图中线段BE、EF、FD之间的数量关系.

解法探究：小明同学通过思考，得到了如下的解决方法.

延长FD到点G，使DG＝BE，连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，从而可得结论.

（1）请先写出小明得出的结论，并在小明的解决方法的提示下，写出所得结论的理由.

解：线段BE、EF、FD之间的数量关系是： .

理由：延长FD到点G，使DG＝BE，连结AG.（以下过程请同学们完整解答）

（2）拓展延伸：

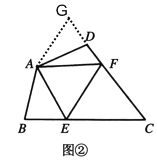
如图②，在四边形ABCD中，AB＝AD，若∠B+∠D＝180°，E、F分别是BC、CD上的点.且∠EAF＝∠BAD，则（1）中的结论是否仍然成立？若成立，请再把结论写一写；若不成立，请直接写出你认为成立的结论.

Answer 1

【答案】（1）EF＝BE＋FD，理由见解析；（2）结论EF＝BE＋FD仍然成立，理由见解析.

【解析】

（1）延长FD到点G．使DG＝BE．连结AG，即可证明△ABE≌△ADG，可得AE＝AG，再证明△AEF≌△AGF，可得EF＝FG，即可解题；

（2）延长FD到点G．使DG＝BE．连结AG，求出∠B＝∠ADG，即可证明△ABE≌△ADG，可得AE＝AG，再证明△AEF≌△AGF，可得EF＝FG，即可解题．

证明：（1）EF＝BE＋FD；

理由：延长FD到点G，使DG＝BE，连结AG.

在△ABE和△ADG中，，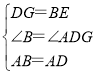

∴△ABE≌△ADG（SAS），

∴AE＝AG，BE＝DG，∠BAE＝∠DAG，

∵∠EAF＝∠BAD，

∴∠GAF＝∠DAG＋∠DAF＝∠BAE＋∠DAF＝∠BAD∠EAF＝∠EAF，

即∠EAF＝∠GAF，

在△AEF和△AGF中，，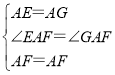

∴△AEF≌△AGF（SAS），

∴EF＝FG，

∵FG＝DG＋DF＝BE＋DF，

∴EF＝BE＋FD；

（2）结论EF＝BE＋FD仍然成立；

理由：如图②，延长FD到点G．使DG＝BE．连结AG，

∵∠B+∠ADF＝180°，∠ADG+∠ADF＝180°，

∴∠B＝∠ADG，

在△ABE和△ADG中，，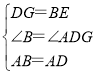

∴△ABE≌△ADG（SAS），

∴AE＝AG，BE＝DG，∠BAE＝∠DAG，

∵∠EAF＝∠BAD，

∴∠GAF＝∠DAG＋∠DAF＝∠BAE＋∠DAF＝∠BAD∠EAF＝∠EAF，

即∠EAF＝∠GAF，

在△AEF和△AGF中，，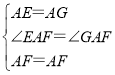

∴△AEF≌△AGF（SAS），

∴EF＝FG，

∵FG＝DG＋DF＝BE＋DF，

∴EF＝BE＋FD.