ЬтФПФкШн
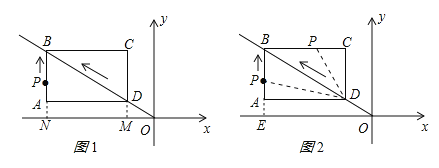
ЁОЬтФПЁПШчЭМ1ЃЌОиаЮABCDЕФСНЬѕБпдкзјБъжсЩЯЃЌЕуDгызјБъдЕуOжиКЯЃЌЧвAD=8ЃЌAB=6ЃЎШчЭМ2ЃЌОиаЮABCDбиOBЗНЯђвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌЭЌЪБЕуPДгAЕуГіЗЂвВвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШбиОиаЮABCDЕФБпABОЙ§ЕуBЯђЕуCдЫЖЏЃЌЕБЕуPЕНДяЕуCЪБЃЌОиаЮABCDКЭЕуPЭЌЪБЭЃжЙдЫЖЏЃЌЩшЕуPЕФдЫЖЏЪБМфЮЊtУыЃЎ
ЃЈ1ЃЉЕБt=5ЪБЃЌЧыжБНгаДГіЕуDЁЂЕуPЕФзјБъЃЛ
ЃЈ2ЃЉЕБЕуPдкЯпЖЮABЛђЯпЖЮBCЩЯдЫЖЏЪБЃЌЧѓГіЁїPBDЕФУцЛ§SЙигкtЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЯргІtЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЕуPдкЯпЖЮABЛђЯпЖЮBCЩЯдЫЖЏЪБЃЌзїPEЁЭxжсЃЌДЙзуЮЊЕуEЃЌЕБЁїPEOгыЁїBCDЯрЫЦЪБЃЌЧѓГіЯргІЕФtжЕЃЎ

ЁОД№АИЁПЃЈ1ЃЉDЃЈЉ4ЃЌ3ЃЉЃЌPЃЈЉ12ЃЌ8ЃЉЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ6ЃЎ
ЃЛЃЈ3ЃЉ6ЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉбгГЄCDНЛxжсгкMЃЌбгГЄBAНЛxжсгкNЃЌдђCMЁЭxжсЃЌBNЁЭxжсЃЌADЁЮxжсЃЌBNЁЮDMЃЌгЩОиаЮЕФаджЪЕУГіКЭЙДЙЩЖЈРэЧѓГіBDЃЌBO=15ЃЌгЩЦНааЯпЕУГіЁїABDЁзЁїNBOЃЌЕУГіБШР§ЪН![]() ЃЌЧѓГіBNЁЂNOЃЌЕУГіOMЁЂDNЁЂPNЃЌМДПЩЕУГіЕуDЁЂPЕФзјБъЃЛ
ЃЌЧѓГіBNЁЂNOЃЌЕУГіOMЁЂDNЁЂPNЃЌМДПЩЕУГіЕуDЁЂPЕФзјБъЃЛ
ЃЈ2ЃЉЕБЕуPдкБпABЩЯЪБЃЌBP=6ЉtЃЌгЩШ§НЧаЮЕФУцЛ§ЙЋЪНЕУГіS=![]() BPADЃЛЂкЕБЕуPдкБпBCЩЯЪБЃЌBP=tЉ6ЃЌЭЌРэЕУГіS=
BPADЃЛЂкЕБЕуPдкБпBCЩЯЪБЃЌBP=tЉ6ЃЌЭЌРэЕУГіS=![]() BPABЃЛМДПЩЕУГіНсЙћЃЛ
BPABЃЛМДПЩЕУГіНсЙћЃЛ
ЃЈ3ЃЉЩшЕуDЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЛЗжСНжжЧщПіЃКЂйЕБЕуPдкБпABЩЯЪБЃЌPЃЈ
ЃЉЃЛЗжСНжжЧщПіЃКЂйЕБЕуPдкБпABЩЯЪБЃЌPЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌгЩ
ЃЉЃЌгЩ![]() КЭ
КЭ![]() ЪБЃЛЗжБ№ЧѓГіtЕФжЕЃЛ
ЪБЃЛЗжБ№ЧѓГіtЕФжЕЃЛ
ЂкЕБЕуPдкБпBCЩЯЪБЃЌPЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЛгЩ
ЃЉЃЛгЩ![]() КЭ
КЭ![]() ЪБЃЌЗжБ№ЧѓГіtЕФжЕМДПЩЃЎ
ЪБЃЌЗжБ№ЧѓГіtЕФжЕМДПЩЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉбгГЄCDНЛxжсгкMЃЌбгГЄBAНЛxжсгкNЃЌШчЭМ1ЫљЪОЃКдђCMЁЭxжсЃЌBNЁЭxжсЃЌADЁЮxжсЃЌBNЁЮDMЃЌЁпЫФБпаЮABCDЪЧОиаЮЃЌЁрЁЯBAD=90ЁуЃЌCD=AB=6ЃЌBC=AD=8ЃЌЁрBD=![]() =10ЃЌЕБt=5ЪБЃЌOD=5ЃЌЁрBO=15ЃЌЁпADЁЮNOЃЌЁрЁїABDЁзЁїNBOЃЌЁр
=10ЃЌЕБt=5ЪБЃЌOD=5ЃЌЁрBO=15ЃЌЁпADЁЮNOЃЌЁрЁїABDЁзЁїNBOЃЌЁр![]() ЃЌМД
ЃЌМД![]() ЃЌЁрBN=9ЃЌNO=12ЃЌЁрOM=12Љ8=4ЃЌDM=9Љ6=3ЃЌPN=9Љ1=8ЃЌЁрDЃЈЉ4ЃЌ3ЃЉЃЌPЃЈЉ12ЃЌ8ЃЉЃЛ
ЃЌЁрBN=9ЃЌNO=12ЃЌЁрOM=12Љ8=4ЃЌDM=9Љ6=3ЃЌPN=9Љ1=8ЃЌЁрDЃЈЉ4ЃЌ3ЃЉЃЌPЃЈЉ12ЃЌ8ЃЉЃЛ
ЃЈ2ЃЉШчЭМ2ЫљЪОЃКЕБЕуPдкБпABЩЯЪБЃЌBP=6ЉtЃЌЁрS=![]() BPAD=
BPAD=![]() ЃЈ6ЉtЃЉЁС8=Љ4t+24ЃЛ
ЃЈ6ЉtЃЉЁС8=Љ4t+24ЃЛ
ЂкЕБЕуPдкБпBCЩЯЪБЃЌBP=tЉ6ЃЌЁрS=![]() BPAB=
BPAB=![]() ЃЈtЉ6ЃЉЁС6=3tЉ18ЃЛ
ЃЈtЉ6ЃЉЁС6=3tЉ18ЃЛ
злЩЯЫљЪіЃК ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЩшЕу DЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЛ
ЃЉЃЛ
ЂйЕБЕуPдкБпABЩЯЪБЃЌPЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌШє
ЃЉЃЌШє![]() ЪБЃЌ
ЪБЃЌ 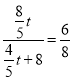 ЃЌНтЕУЃКt=6ЃЛ
ЃЌНтЕУЃКt=6ЃЛ
Шє![]() ЪБЃЌ
ЪБЃЌ 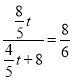 ЃЌНтЕУЃКt=20ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЛ
ЃЌНтЕУЃКt=20ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЛ
ЂкЕБЕуPдкБпBCЩЯЪБЃЌPЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌШє
ЃЉЃЌШє![]() ЪБЃЌ
ЪБЃЌ 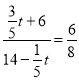 ЃЌНтЕУЃКt=6ЃЛ
ЃЌНтЕУЃКt=6ЃЛ
Шє![]() ЪБЃЌ
ЪБЃЌ 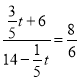 ЃЌНтЕУЃК
ЃЌНтЕУЃК ![]() ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЛ
ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЛ
злЩЯЫљЪіЃКЕБt=6ЪБЃЌЁїPEOгыЁїBCDЯрЫЦЃЎ