题目内容
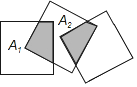
【题目】如图,三个边长均为1的正方形按如图所示的方式摆放,A1,A2分别是正方形对角线的交点,则重叠部分的面积和为______.
【答案】![]()
【解析】
过点A1分别作正方形两边的垂线A1D与A1E,根据正方形的性质可得A1D=A1E,再根据同角的余角相等求出∠BA1D=∠CA1E,然后利用“角边角”证明△A1BD和△A1CE全等,根据全等三角形的面积相等求出阴影部分的面积等于正方形面积的![]() ,即可求解.
,即可求解.
如图,过点A1分别作正方形两边的垂线A1D与A1E,
∵点A1是正方形的中心,
∴A1D=A1E,
∵∠BA1D+∠BA1E=90°,∠CA1E+∠BA1E=90°,
∴∠BA1D=∠CA1E,A1D=A1E,∠A1DB=∠A1EC=90°,
∴△A1BD≌△A1CE(ASA),
∴△A1BD的面积=△A1CE的面积,
∴两个正方形的重合面积=![]() 正方形面积=
正方形面积=![]() ,
,
∴重叠部分的面积和为![]() ×2=
×2=![]() .
.
故答案是:![]() .
.

【题目】随着教育教学改革的不断深入,应试教育向素质教育转轨的力度不断加大,体育中考已成为初中毕业升学考试的重要内容之一。为了解某市九年级学生中考体育成绩情况,现从中随机抽取部分考生的体育成绩进行调查,并将调查结果绘制如下图表:
2019年中考体育成绩(分数段)统计表 | ||
分数段 | 频数(人) | 频率 |
25≤x<30 | 12 | 0.05 |
30≤x<35 | 24 | b |
35≤x<40 | 60 | 0.25 |
40≤x<45 | a | 0.45 |
45≤x<50 | 36 | 0.15 |
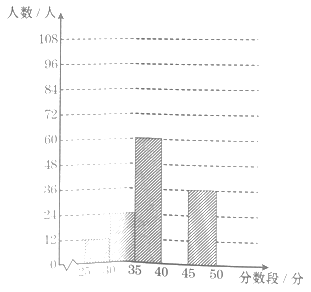
根据上面提供的信息,回答下列问题:
(1)表中a和b所表示的数分别为a=______,b=______;并补全频数分布直方图;
(2)甲同学说“我的体育成绩是此次抽样调查所得数据的中位数。”请问:甲同学的体育成绩在______分数段内?
(3)如果把成绩在40分以上(含40分)定为优秀那么该市12000名九年级考生中考体育成绩为优秀的约有多少名?