题目内容
【题目】阅读下列一段文字,然后回答下列问题:
已知平面内两点P1(x1,y1),P2(x2,y2),其两点间的距离![]() 。例如:已知P(3,1),Q(1,-2),则这两点间的距离
。例如:已知P(3,1),Q(1,-2),则这两点间的距离![]() .特别地,如果两点M(x1,y1),N(x2,y2),所在的直线与坐标轴重合或平行于坐标轴或者垂直于坐标轴,那么这两点间的距离公式可简化为
.特别地,如果两点M(x1,y1),N(x2,y2),所在的直线与坐标轴重合或平行于坐标轴或者垂直于坐标轴,那么这两点间的距离公式可简化为![]() 或
或![]() 。
。
(1)已知A(2,3),B(-1,-2),则A,B两点间的距离为_________;
(2)已知M,N在平行于y轴的直线上,点M的纵坐标为-2,点N的纵坐标为3,则M,N两点间的距离为_________;
(3)在平面直角坐标系中,已知A(0,4),B(4,2),在x轴上找点P,使PA+PB的长度最短,求出点P的坐标及PA+PB的最短长度.

【答案】(1)![]() ;(2)5;(3) PA+PB的长度最短时,点P的坐标为(
;(2)5;(3) PA+PB的长度最短时,点P的坐标为(![]() ,0),PA+PB的最短长度为
,0),PA+PB的最短长度为![]() .
.
【解析】
(1)直接利用两点之间距离公式直接求出即可;
(2)根据题意列式计算即可;
(3)利用轴对称求最短路线方法得出P点位置,进而求出PA+PB的最小值.
(1) (1)∵A(2,3),B(-1,-2),
∴A,B两点间的距离为:![]() ;
;
(2) ∵M,N在平行于y轴的直线上,点M的纵坐标为-2,点N的纵坐标为3,
则M,N两点间的距离为3-(-2)=5;
(3)如图,作点A关于x轴的对称点A′,连接A′B与x轴交于点P,此时PA+PB最短
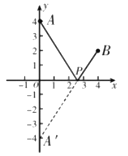
设A′B的解析式为y=kx+b
将A′(0,-4),B(4,2)代入y=kx+b得
![]() 解得
解得
∴直线设A′B的解析式为![]()
令y=0得![]()
∴P(0,![]() ).
).
∵PA′=PA
∴PA+PB=PA′+PB=A′B=![]()
∴PA+PB的长度最短时,点P的坐标为(![]() ,0),PA+PB的最短长度为
,0),PA+PB的最短长度为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目