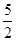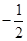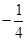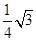题目内容
如图, ABCD 中,AE⊥BC于E,AF⊥CD于F,若AE=4,AF=6,sin∠BAE=
ABCD 中,AE⊥BC于E,AF⊥CD于F,若AE=4,AF=6,sin∠BAE=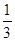 ,则CF= .
,则CF= .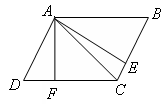
 ABCD 中,AE⊥BC于E,AF⊥CD于F,若AE=4,AF=6,sin∠BAE=
ABCD 中,AE⊥BC于E,AF⊥CD于F,若AE=4,AF=6,sin∠BAE=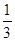 ,则CF= .
,则CF= .
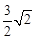 。
。由AE⊥BC和sin∠BAE=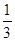 ,得
,得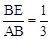 。∴可设BE=k,则AB=3k。
。∴可设BE=k,则AB=3k。
∵AE=4,∴根据勾股定理得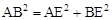 ,即
,即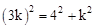 ,解得
,解得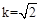 (负值已舍去)。
(负值已舍去)。
∴BE=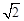 , AB=3
, AB=3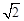 。
。
∵四边形ABCD是平行四边形,∴DC=AB==3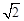 ,∠D=∠B。
,∠D=∠B。
又∵AE⊥BC,AF⊥CD,∴∠AFD=∠AEB=900。∴△AFD∽△AEB。∴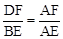 。
。
又∵AF=6,∴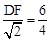 ,解得
,解得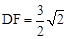 。∴CF=DC-DF=
。∴CF=DC-DF=  。
。
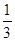 ,得
,得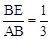 。∴可设BE=k,则AB=3k。
。∴可设BE=k,则AB=3k。∵AE=4,∴根据勾股定理得
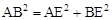 ,即
,即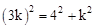 ,解得
,解得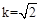 (负值已舍去)。
(负值已舍去)。∴BE=
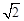 , AB=3
, AB=3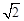 。
。∵四边形ABCD是平行四边形,∴DC=AB==3
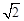 ,∠D=∠B。
,∠D=∠B。又∵AE⊥BC,AF⊥CD,∴∠AFD=∠AEB=900。∴△AFD∽△AEB。∴
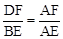 。
。又∵AF=6,∴
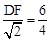 ,解得
,解得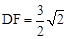 。∴CF=DC-DF=
。∴CF=DC-DF=  。
。
练习册系列答案
相关题目

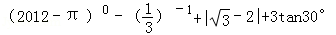 .
.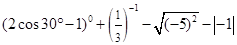
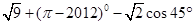

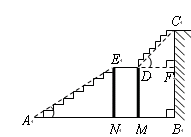
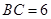 米,
米,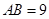 米,中间平台宽度
米,中间平台宽度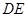 为2米,
为2米,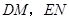 为平台的两根支柱,
为平台的两根支柱,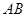 ,垂足分别为
,垂足分别为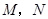 ,
,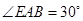 ,
,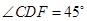 .求
.求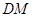 和
和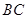 的水平距离
的水平距离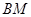 .(精确到0.1米,参考数据:
.(精确到0.1米,参考数据: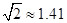 ,
,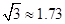 )
)
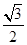 cos30°+
cos30°+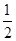 sin30°-tan60°·sin60°=( )
sin30°-tan60°·sin60°=( )