题目内容
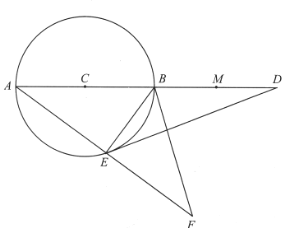
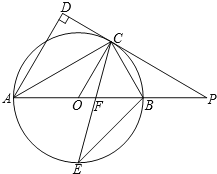
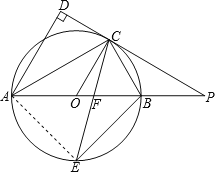
【题目】如图，AB是⊙O的直径，点C是⊙O上一点，AD与过点C的切线垂直，垂足为点D，直线DC与AB的延长线相交于点P，弦CE平分∠ACB，交AB于点F，连接BE．
（1）求证：AC平分∠DAB；
（2）求证：△PCF是等腰三角形；
（3）若tan∠ABC= 
，求线段PC的长．
【答案】（1）见解析；（2）见解析；（3）24
【解析】
（1）由PD切⊙O于点C，AD与过点C的切线垂直，易证得OC∥AD，继而证得AC平分∠DAB；
（2）由AD⊥PD，AB为⊙O的直径，易证得CE平分∠ACB，继而可得∴∠PFC=∠PCF，即可证得PC=PF，即△PCF是等腰三角形；
（3）首先连接AE，易得AE=BE，即可求得AB的长，继而可证得△PAC∽△PCB，又由tan∠ABC=
，BE=7
，即可求得答案．
（1）∵PD切⊙O于点C，
∴OC⊥PD．
又∵AD⊥PD，
∴OC∥AD．
∴∠ACO=∠DAC．
又∵OC=OA，
∴∠ACO=∠CAO，
∴∠DAC=∠CAO，
即AC平分∠DAB．
（2）∵AD⊥PD，
∴∠DAC+∠ACD=90°．
又∵AB为⊙O的直径，
∴∠ACB=90°．
∴∠PCB+∠ACD=90°，
∴∠DAC=∠PCB．
又∵∠DAC=∠CAO，
∴∠CAO=∠PCB．
∵CE平分∠ACB，
∴∠ACF=∠BCF，
∴∠CAO+∠ACF=∠PCB+∠BCF，
∴∠PFC=∠PCF，
∴PC=PF，
∴△PCF是等腰三角形．
（3）连接AE．
∵CE平分∠ACB，
∴
．
∵AB为⊙O的直径，
∴∠AEB=90°．
在Rt△ABE中，AB＝
＝14．
∵∠PAC=∠PCB，∠P=∠P，
∴△PAC∽△PCB，
∴
．
又∵tan∠ABC=，
∴
．
设PC=4k，PB=3k，则在Rt△POC中，PO=3k+7，OC=7，
∵PC2+OC2=OP2，
∴（4k）2+72=（3k+7）2，
∴k=6（k=0不合题意，舍去）．
∴PC=4k=4×6=24．
