题目内容
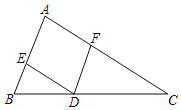
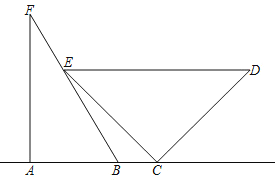
【题目】如图,在△ABC中,∠A=90°,点D为BC的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,试写出线段BE,EF,FC之间的数量关系,并说明理由.

【答案】FC2+BE2=EF2.
【解析】
BE2+CF2=EF2,可延长FD至P,使DP=DF,连接EP,连接BP,证明△CFD≌BPD,进而在Rt△PBE中,由勾股定理即可得出结论.
BE2+CF2=EF2.理由如下:
延长FD至P,使DP=DF,连接EP,BP.
∵D是BC的中点,∴BD=CD.
在△CDF和△BPD中,∵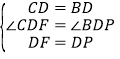 ,∴△CDF≌△BPD(SAS),∴CF=BP,∠C=∠PBD.
,∴△CDF≌△BPD(SAS),∴CF=BP,∠C=∠PBD.
∵∠A=90°,∴∠ABP=∠ABC+∠DBP=∠ABC+∠C=180°﹣90°=90°.
∵DE⊥DF,DF=DP,∴EF=FP(垂直平分线上的点到线段两端点距离相等).在Rt△BEP中,由勾股定理得:BE2+BP2=EP2=EF2,即:BE2+CF2=EF2.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目