��Ŀ����
����Ŀ��С����С������Ϸ����ͼ��������ͬ�Ŀ�Ƭ��ÿ�����ţ���һ�鿨Ƭ����ֱ��������1��3��5���ڶ��鿨Ƭ����ֱ��������2��4��6�����ǽ���Ƭ���泯�ϣ�������ϴ�Ⱥ�ÿ�鿨Ƭ�и�����һ�ţ���Ϊһ����Ϸ�������������ſ�Ƭ����������֮��С��10����С����ʤ�������������ſ�Ƭ����������֮������10����С����ʤ������Ϊ�����Ϸ�����˫����ƽ����˵�����ɣ�

���𰸡������Ϸ�����˫����ƽ�����ɼ�����.
��������
����״ͼչʾ����9�ֵȿ��ܵĽ���������ҳ����������ſ�Ƭ����������֮��С��10�Ľ���������������ſ�Ƭ����������֮������10�Ľ������Ȼ����ݸ��ʹ�ʽ���������С����ʤ�ĸ��ʺ�С����ʤ�ĸ��ʣ���ͨ���Ƚ������ʵĴ�С�ж���Ϸ�Ƿ�ƽ.
���������Ϸ�����˫����ƽ���������£�
����״ͼΪ��
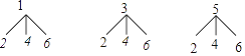
����9�ֵȿ��ܵĽ�������������������ſ�Ƭ����������֮��С��10�Ľ����Ϊ4�����������ſ�Ƭ����������֮������10�Ľ����Ϊ4��
����С����ʤ�ĸ���=![]() ��С����ʤ�ĸ���=
��С����ʤ�ĸ���=![]() .
.
���������Ϸ�����˫����ƽ.
�ʴ�Ϊ�������Ϸ�����˫����ƽ�����ɼ�����.

 53���ò�ϵ�д�
53���ò�ϵ�д�����Ŀ��С����С����λͬѧ��ѧϰ�����ʡ�ʱ����Ͷ�����ӣ��ʵؾ��ȵ������壩ʵ�飬���ǹ�����60�����飬ʵ��Ľ�����£�
���ϵ��� | 1 | 2 | 3 | 4 | 5 | 6 |
���ִ��� | 7 | 9 | 6 | 8 | 20 | 10 |
��1�����㡰2�㳯�ϡ���Ƶ�ʺ͡�5�㳯�ϡ���Ƶ�ʣ�
��2��С��˵��������ʵ�飬һ��ʵ���г���3�㳯�ϵĸ�����![]() ����С������һ˵����ȷ��Ϊʲô��
����С������һ˵����ȷ��Ϊʲô��
��3��С��˵���������600�Σ���ô����6�㳯�ϵĴ���������100�Σ���С�յ���һ˵����ȷ��Ϊʲô��