Question

【题目】已知：如图，四边形ABCD为矩形，，，点E是CD的中点，点P在AB上以每秒2个单位的速度由A向B运动，设运动时间为t秒．

（1）当点P在线段AB上运动了t秒时，__________________（用代数式表示）;

（2）t为何值时，四边形PDEB是平行四边形：

（3）在直线AB上是否存在点Q，使以D、E、Q、P四点为顶点的四边形是菱形？若存在，求出t的值：若不存在，说明理由．

Answer 1

【答案】（1）；（2）当时，四边形PDEB是平行四边形；（3）t的值为或或．

【解析】

（1）求出PA，根据线段和差定义即可解决问题．

（2）根据，构建方程即可解决问题．

（3）①当时，可得四边形DEPQ，四边形是菱形，②当时，可得四边形是菱形，分别求解即可解决问题．

解：（1），，

，

故答案为．

（2）当时，四边形PDEB是平行四边形，

，

，

答：当时，四边形PDEB是平行四边形．

（3）存在．

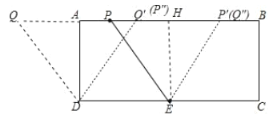
①当时，可得四边形DEPQ，四边形是菱形，

作于H．

在中，，，

，

或，

或时，可得四边形DEPQ，四边形是菱形．

②当时，可得四边形是菱形，易知：，

，

综上所述，满足条件的t的值为或或．