题目内容
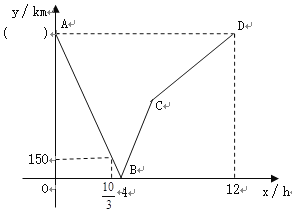
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图像回答以下问题:
(1)请在图中的( )内填上正确的值,并写出两车的速度和.
(2)求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围.
(3)请直接写出两车之间的距离不超过15km的时间范围.
【答案】(1)900;225km∕h.(2)yBC=225x-900(4≤x≤6);(3)![]()
【解析】试题分析:(1)设直线![]() 的解析式为:
的解析式为: ![]() 把点
把点![]() 代入,求出解析式,当
代入,求出解析式,当![]() 时,
时, ![]() 4小时后两车相遇,即可求出它们的速度和.
4小时后两车相遇,即可求出它们的速度和.
(2)由函数图象的数据,根据速度=路程÷时间就可以得出慢车的速度,由相遇问题求出速度和就可以求出快车的速度,由快车的速度求出快车走完全程的时间就可以求出点C的横坐标,由两车的距离=速度和×时间就可以求出C点的纵坐标,由待定系数法就可以求出结论.
![]() 分别让
分别让![]() 解析式中的
解析式中的![]() 即可求出两车之间的距离不超过15km的时间范围.
即可求出两车之间的距离不超过15km的时间范围.
试题解析:(1)设直线![]() 的解析式为:
的解析式为: ![]() 把点
把点![]() 代入得:
代入得:
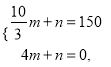
解得: ![]()
直线![]() 的解析式为:
的解析式为: ![]()
当![]() 时,
时, ![]()
图中括号里应填900,两车的速度和为: ![]()
(2)快车与慢车的速度和为:900÷4=225km/h,
慢车的速度为:900÷12=75km/h,
快车的速度为:22575=150km/h.
由题意得快车走完全程的时间为:900÷150=6h,
6时时两车之间的距离为:225×(64)=450km.
则C(6,450).
设线段BC的解析式为y=kx+b,由题意,得
![]()
解得: ![]()
则y=225x900,自变量x![]()
(3)![]()

练习册系列答案
相关题目