题目内容
【题目】定义:对角线互相垂直的凸四边形叫做“垂直四边形”.
(1)理解:
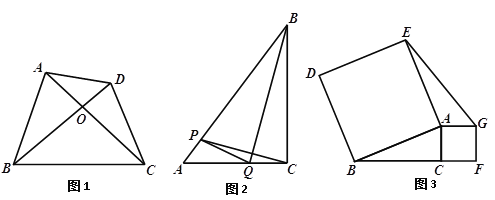
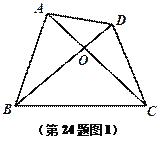
如图1,已知四边形ABCD是“垂直四边形”,对角线AC,BD交于点O,AC=8,BD=7,求四边形ABCD的面积.
(2)探究:
小明对 “垂直四边形”ABCD(如图1)进行了深入探究,发现其一组对边的平方和等于另一组对边的平方和.即![]() .你认为他的发现正确吗?试说明理由.
.你认为他的发现正确吗?试说明理由.
(3)应用:
① 如图2,在△ABC中, ![]() ,AC=6,BC=8,动点P从点A出发沿AB方向以每秒5个单位的速度向点B匀速运动,同时动点Q从点C出发沿CA方向以每秒6个单位的速度向点A匀速运动,运动时间为t秒(
,AC=6,BC=8,动点P从点A出发沿AB方向以每秒5个单位的速度向点B匀速运动,同时动点Q从点C出发沿CA方向以每秒6个单位的速度向点A匀速运动,运动时间为t秒(![]() ),连结CP,BQ,PQ.当四边形BCQP是“垂直四边形”时,求t的值.
),连结CP,BQ,PQ.当四边形BCQP是“垂直四边形”时,求t的值.
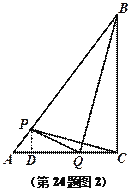
② 如图3,在△ABC中,![]() ,AB=3AC,分别以AB,AC为边向外作正方形ABDE和正方形ACFG,连结EG.请直接写出线段EG与BC之间的数量关系.
,AB=3AC,分别以AB,AC为边向外作正方形ABDE和正方形ACFG,连结EG.请直接写出线段EG与BC之间的数量关系.
【答案】(1)28;(2)证明见解析;(3)①![]() ;②
;②![]()
【解析】试题分析:(1)由于对角线互相垂直,所以四边形ABCD的面积可化为![]() AOBD+
AOBD+![]() COBD的和;
COBD的和;
(2)由于对角线互相垂直,由勾股定理分别表示出AB2、CD2、AD2、BC2;
(3)①过点P作PD⊥AC于点D,构造△PAD∽△BAC后,利用BP2+CQ2=PQ2+BC2列出关于t的方程;②连接BE、CG、BG、CE,证明四边形BCGE是垂直四边形,然后利用其性质“一组对边的平方和等于另一组对边的平方和”,即可得出EG与BC的数量关系.
试题解析:(1)∵四边形ABCD是“垂直四边形”,
∴AC⊥BD,
∴四边形ABCD的面积为![]() AOBD+
AOBD+![]() COBD=
COBD=![]() BD(AO+CO) =
BD(AO+CO) =![]() ACBD=
ACBD=![]() 2×8×7=28,
2×8×7=28,
故答案为:28;
(2)∵四边形ABCD是“垂直四边形”,
∴AC⊥BD.
由勾股定理可知:
AB2+CD2=(AO2+BO2)+(DO2+CO2),
AD2+BC2=(AO2+DO2)+(BO2+CO2),
∴AB2+CD2=AD2+BC2;
(3)① 过点P作PD⊥AC于点D,
∵∠ACB=90°,
∴AB=![]() =10,PD∥BC.
=10,PD∥BC.
∴ △PAD∽△BAC,
∴![]() .
.
∵ 动点P的速度为每秒5个单位,动点Q的速度为每秒6个单位.
∴ AP=5t,CQ=6t
∴![]() ,∴AD=3t,PD=4t.
,∴AD=3t,PD=4t.
∵ 四边形BCQP是“垂直四边形”.
∴BP2+CQ2=PQ2+BC2.
∴(10-5t)2+(6t)2=(4t)2+(6-9t)2+82,
解得t=![]() 或t=0(舍去).
或t=0(舍去).
∴ 当四边形BCQP是“垂直四边形”时,t的值为![]() .
.
②如图3,
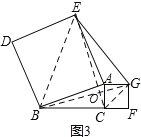
连接CG、BG、BE、CE,
CE与BG交于点O
由题意知:EA=BA,AC=AG
∠EAB=∠CAG=90°
∴∠EAB+∠BAC=∠CAG+∠BAC
∴∠EAC=∠BAG
在△EAC与△BAG中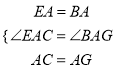 ,
,
∴△EAC≌△BAG(SAS)
∴∠CEA=∠GBA
∴∠EAB=∠BOE=90°
∴四边形BCGE是“垂直四边形”
∴BC2+EG2=BE2+CG2,
∵AB=3AC,
∴EG2=![]() BC2.
BC2.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案【题目】如图1是流花河的水文资料(单位:米),取河流的警戒水位作为0点,那么图中的其他数据可以分别记作什么?如表是小明记录的今年雨季流花河一周内水位变化情况(上周末的水位达到警戒水位)
星期 水位 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化/米 | +0.2 | +0.8 | -0.4 | +0.1 | +0.3 | -0.4 | -0.1 |
实际水位/米 | 33.6 |
注:正表示水位比前一天上升,负表示水位比前一天下降.

(1)本周星期______河流的水位最高,水位在警戒水位之______(上或下);星期______河流的水位最低,水位在警戒水位之______(上或下);
(2)与上周相比,本周末河流水位是______(上升了或下降了);
(3)完成上面的实际水位记录;
(4)以警戒水位为0点,用折线统计图(如图2)表示本周的水位情况.
【题目】阅读下列材料:
根据联合国《人口老龄化及其社会经济后果》中提到的标准,当一个国家或地区65岁及以上老年人口数量占总人口比例超过7%时,意味着这个国家或地区进入老龄化。从经济角度,一般可用“老年人口抚养比”来反映人口老龄化社会的后果。所谓“老年人口抚养比”是指某范围人口中,老年人口数(65岁及以上人口数)与劳动年龄人口数(15-64岁人口数)之比,通常用百分比表示,用以表明每100名劳动年龄人口要负担多少名老年人。
以下是根据我国近几年的人口相关数据制作的统计图和统计表。
2011-2014年全国人口年龄分布图

2011-2014年全国人口年龄分布表
2011年 | 2012年 | 2013年 | 2014年 | |
0-14岁人口占总人口的百分比 | 16.4% | 16.5% | 16.4% | 16.5% |
15-64岁人口占总人口的百分比 | 74.5% | 74.1% | 73.9% | 73.5% |
65岁及以上人口占总人口的百分比 | m | 9.4% | 9.7% | 10.0% |
*以上图表中数据均为年末的数据。
根据以上材料解答下列问题:
(1)2011年末,我国总人口约为_______亿,全国人口年龄分布表中m的值为_______;
(2)若按目前我国的人口自然增长率推测,到2027年末我国约有14.60亿人。假设0-14岁人口占总人口的百分比一直稳定在16.5%,15-64岁的人口一直稳定在10亿,那么2027年末我国0-14岁人口约为_______亿,“老年人口抚养比”约为_______; (精确到1%)
(3)2016年1月1日起我国开始施行“全面二孩”政策,一对夫妻可生育两个孩子。在未来10年内,假设出生率显著提高,这_______(填“会”或“不会”)对我国的“老年人口抚养比”产生影响。