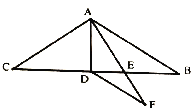
题目内容
【题目】已知![]() 为等边三角形,点
为等边三角形,点![]() 为直线
为直线![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 、点
、点![]() 重合).连接
重合).连接![]() ,以
,以![]() 为边向逆时针方向作等边
为边向逆时针方向作等边![]() ,连接
,连接![]() ,
,
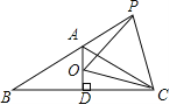
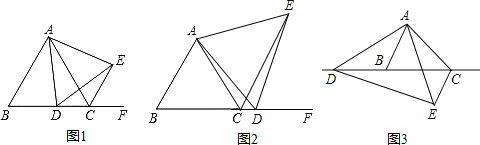
(1)如图1,当点![]() 在边
在边![]() 上时:
上时:
①求证:![]() ;
;
②判断![]() 之间的数量关系是 ;
之间的数量关系是 ;
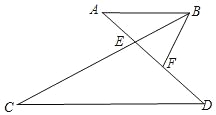
(2)如图2,当点![]() 在边
在边![]() 的延长线上时,其他条件不变,判断
的延长线上时,其他条件不变,判断![]() 之间存在的数量关系,并写出证明过程;
之间存在的数量关系,并写出证明过程;
(3)如图3,当点![]() 在边
在边![]() 的反向延长线上时,其他条件不变,请直接写出
的反向延长线上时,其他条件不变,请直接写出![]() 之间存在的数量关系为 .
之间存在的数量关系为 .
【答案】(1)①见解析;②AC=CE+CD;(2)CE=AC+CD,证明见解析;(3)CD=CE+AC.
【解析】
(1)①根据等边三角形的性质就可以得出∠BAC=∠DAE=60°,AB=AC,AD=AE,进而就可以得出△ABD≌△ACE;②由△ABD≌△ACE就可以得出AC=BC=CD+CE;
(2)同(1)先证明△ABD≌△ACE,从而可得出BD=BC+CD=AC+CD=CE;
(3)同(1)先证明△ABD≌△ACE,从而可得出CE+AC=CD.
解:(1)①∵△ABC和△ADE是等边三角形,
∴∠BAC=∠DAE=60°,AB=BC=AC,AD=DE=AE.
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠BAD=∠EAC.
在△ABD和△ACE中
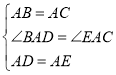 ,
,
∴△ABD≌△ACE(SAS).
②∵△ABD≌△ACE,
∴BD=CE.
∵BC=BD+CD,
∴BC=CE+CD,
∴AC=CE+CD,
故答案为:AC=CE+CD;
(2)AC+CD=CE.证明如下:
∵△ABC和△ADE是等边三角形,
∴∠BAC=∠DAE=60°,AB=BC=AC,AD=DE=AE.
∴∠BAC+∠DAC=∠DAE+∠DAC,
∴∠BAD=∠EAC.
在△ABD和△ACE中
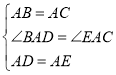 ,
,
∴△ABD≌△ACE(SAS).
∴BD=CE.
∵BD=BC+CD,
∴CE=AC+CD;
(3)DC=CE+BC.证明如下:
∵△ABC和△ADE是等边三角形,
∴∠BAC=∠DAE=60°,AB=BC=AC,AD=DE=AE.
∴∠BAC-∠BAE=∠DAE-∠BAE,
∴∠BAD=∠EAC.
在△ABD和△ACE中
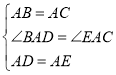 ,
,
∴△ABD≌△ACE(SAS).
∴BD=CE.
∵CD=BD+BC,
∴CD=CE+AC.
故答案为:CD=CE+AC.

 中考解读考点精练系列答案
中考解读考点精练系列答案