题目内容
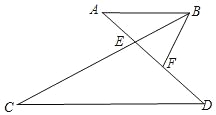
【题目】如图,已知AB∥CD,AD、BC相交于点E,点F在ED上,且∠CBF=∠D.
(1)求证:FB2=FEFA;
(2)若BF=3,EF=2,求△ABE与△BEF的面积之比.
【答案】(1)证明见解析;(2)5:4.
【解析】
试题分析:(1)要证明FB2=FEFA,只要证明△FBE∽△FAB即可,根据题目中的条件可以找到两个三角形相似的条件,本题得以解决;
(2)根据(1)中的结论可以得到AE的长,然后根据△ABE与△BEF如果底边分别为AE和EF,则底边上的高相等,面积之比就是AE和EF的比值.
试题解析:(1)∵AB∥CD,
∴∠A=∠D.
又∵∠CBF=∠D,
∴∠A=∠CBF,
∵∠BFE=∠AFB,
∴△FBE∽△FAB,
∴![]()
∴FB2=FEFA;
(2)∵FB2=FEFA,BF=3,EF=2
∴32=2×(2+AE)
∴![]()
∴![]() ,
,
∴△ABE与△BEF的面积之比为5:4.

练习册系列答案
相关题目