题目内容
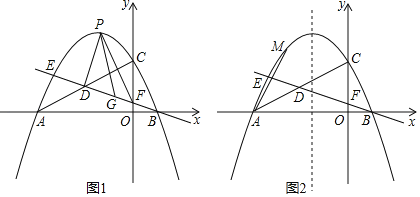
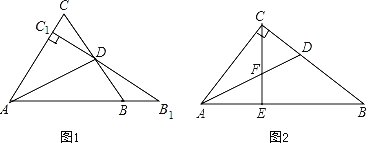
【题目】如图(1)所示:等边△ABC中,线段AD为其内角角平分线,过D点的直线B1C1⊥AC于C1交AB的延长线于B1.
(1)请你探究:![]() ,
,![]() 是否都成立?
是否都成立?
(2)请你继续探究:若△ABC为任意三角形,线段AD为其内角角平分线,请问![]() 一定成立吗?并证明你的判断.
一定成立吗?并证明你的判断.
(3)如图(2)所示Rt△ABC中,∠ACB=90,AC=8,BC=![]() ,DE∥AC交AB于点E,试求
,DE∥AC交AB于点E,试求![]() 的值.
的值.
【答案】(1)成立,理由见解析;(2)成立,理由见解析;(3)![]()
【解析】
(1)根据等边三角形的性质得到AD垂直平分BC,∠CAD=∠BAD=30°,AB=AC,则DB=CD,易得![]() ;由于∠C1AB1=60°,得∠B1=30°,则AB1=2AC1,同理可得到DB1=2DC1,易得
;由于∠C1AB1=60°,得∠B1=30°,则AB1=2AC1,同理可得到DB1=2DC1,易得![]() ;
;
(2)过B点作BE∥AC交AD的延长线于E点,根据平行线的性质和角平分线的定义得到∠E=∠CAD=∠BAD,则BE=AB,并且根据相似三角形的判定得△EBD∽△ACD,得到![]() ,而BE=AB,于是有
,而BE=AB,于是有![]() ,这实际是三角形的角平分线定理;
,这实际是三角形的角平分线定理;
(3)AD为△ABC的内角角平分线,由(2)的结论,根据相似三角形的判定得△DEF∽△ACF,利用相似三角形的性质解答即可.
解:(1)![]() 等边△ABC中,线段AD为其内角角平分线,
等边△ABC中,线段AD为其内角角平分线,
![]()
![]()
因为B1C1⊥AC于C1交AB的延长线于B1,
![]() ∠CAB=60°,∠B1=∠CAD=∠BAD=30°,
∠CAB=60°,∠B1=∠CAD=∠BAD=30°,
![]() AD=B1D,
AD=B1D,![]()
![]()
![]()
综上:这两个等式都成立;

(2)可以判断结论仍然成立,证明如下:
如图所示,△ABC为任意三角形,过B点作BE∥AC交AD的延长线于E点,
线段AD为其内角角平分线

![]() ∠E=∠CAD=∠BAD,△EBD∽△ACD
∠E=∠CAD=∠BAD,△EBD∽△ACD
∴BE=AB,![]()
又∵BE=AB.
∴![]() ,
,
即对任意三角形结论仍然成立;
(3)如图(2)所示,因为Rt△ABC中,∠ACB=90°,AC=8,![]() ,
,
![]()

∵AD为△ABC的内角角平分线,
∴
∵DE∥AC,
![]()
![]()
∵DE∥AC,
∴△DEF∽△ACF,![]()
∴![]()
![]()
![]()
![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案