Question

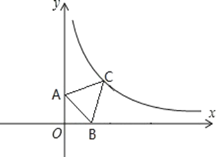
【题目】一次函数y1=kx+b与反比例函数y2=（n＞0）交于点A（1，3），B（3，m）．

（1）分别求两个函数的解析式；

（2）根据图像直接写出，当x为何值时，y1＜y2；

（3）在x轴上找一点P，使得△OAP的面积为6，求出P点坐标．

Answer 1

【答案】（1）y2=，y1=-x+4．（2）x＜1或x＞3．（3）（-4，0）或（4，0）．

【解析】

（1）首先将A，B两点坐标代入反比例函数解析式，得出m，n的值，在利用待定系数法即可解决问题；

（2）观察图象，写出一次函数的图象在反比例函数图象下方时，x的取值范围即可；

（3）由题意可知A的纵坐标的值即为△OAP的高，且P点在横轴上，根据三角形的面积公式可知OP的长为4，写出可能的坐标即可．

解：（1）将A（1，3），代入y2=（n＞0），得n=3，

再将B（3，m）代入y2=，得m=1，

所以将A，B两点坐标代入y1=kx+b，

得，

解得，

∴一次函数解析式为y1=-x+4；

（2）根据题意的一次函数的图象在反比例函数图象下方时所对应的x的取值范围即为所求，此时x的范围是：x＜1或x＞3；

（3）由题意得△OAP的高为3

∴S△OAP=·3·|OP|=6，

∴OP的长为4，

又∵点P在x轴上，

∴点P的坐标为（-4，0）或（4，0）．