题目内容
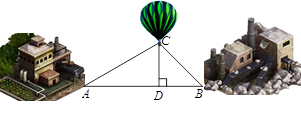
一艘轮船自南向北航行,在A处测得北偏西21.3º方向有一座小岛C,继续向北航行60海里到达B处,测得小岛C此时在轮船的北偏西63.5º方向上.之后,轮船继续向北航行多少海里,距离小岛C最近?(参考数据:sin21.3º≈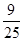 ,tan21.3º≈
,tan21.3º≈ ,sin63.5º≈
,sin63.5º≈ ,tan63.5º≈2)
,tan63.5º≈2)

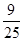 ,tan21.3º≈
,tan21.3º≈ ,sin63.5º≈
,sin63.5º≈ ,tan63.5º≈2)
,tan63.5º≈2)
15.
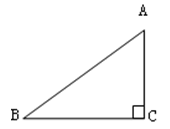
试题分析:过C作AB的垂线,交直线AB于点D,得到Rt△ACD与Rt△BCD,在直角△BCD中,即可利用BD表示出CD的长,再在直角△ACD中,利用三角函数即可求解.
试题解析:过C作AB的垂线,交直线AB于点D,得到Rt△ACD与Rt△BCD.
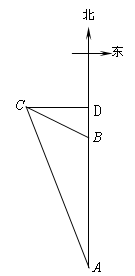
设BD=x海里,
在直角△BCD中,CD=BD•tan∠CBD=x•tan63.5°,
在直角△ACD中,AD=AB+BD=(60+x)海里,tan∠A=
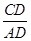 ,
,∴CD=(60+x)•tan21.3°,
∴x•tan63.5°=(60+x)tan21.3°,
即2x=
 (60+x),
(60+x),解得:x=15,
答:轮船继续向北航行15海里,距离小岛C最近.
考点: 解直角三角形的应用-方向角问题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目
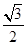 .计算
.计算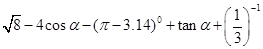 的值.
的值.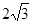 ,求AB的长.
,求AB的长.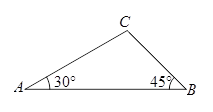
 ,AD=4.
,AD=4.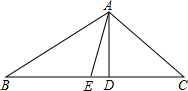
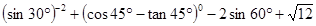 .
.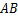 的坡比
的坡比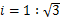 (指坡面的铅直高度与水平宽度的比),且
(指坡面的铅直高度与水平宽度的比),且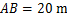 .身高为
.身高为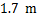 的小明站在大堤
的小明站在大堤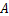 点,测得高压电线杆端点
点,测得高压电线杆端点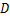 的仰角为
的仰角为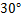 .已知地面
.已知地面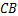 宽
宽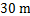 ,求高压电线杆
,求高压电线杆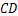 的高度(结果保留三个有效数字,
的高度(结果保留三个有效数字,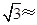 1.732).
1.732).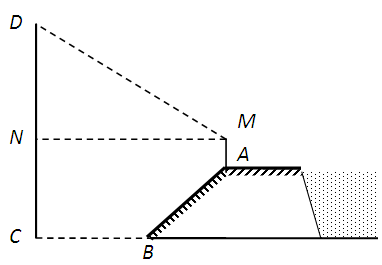
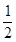 ;
; ;
; .
.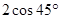 = .
= .