题目内容
【题目】如图，在□ABCD中，点E在边AD上，以BE为折痕，将△ABE向上翻折，点A正好落在CD上的点F处，若△FDE的周长为8，△FCB的周长为22，则□ABCD的周长为________，FC的长为________．
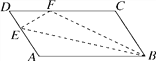
【答案】 30 7
【解析】试题解析：由折叠的性质可得EF=AE、BF=BA，
∴ABCD的周长=DF+FC+CB+BA+AE+DE=△FDE的周长+△FCB的周长=30，
设DF=x，FC=y，
∵ABCD，
∴AD=BC，CD=AB，
∵BE为折痕，
∴AE=EF，AB=BF，
∵△FDE的周长为8，△FCB的周长为22，
∴BC=AD=8x，AB=CD=x+y，
∴y+x+y+8x=22，
解得y=7.
故答案为：30,7.
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
【题目】某停车场收费标准分为中型汽车和小型汽车两种，某两天这个停车场的收费情况如下表：
中型汽车数量 | 小型汽车数量 | 收取费用 | |
第一天 | 15辆 | 35辆 | 360元 |
第二天 | 18辆 | 20辆 | 300元 |
（1）中型汽车和小型汽车的停车费每辆多少元？
（2）某天停车场共停车70辆，若收取的停车费用高于500元，则中型汽车至少有多少辆？
