题目内容
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴相交于A、B两点,与y轴相交于点C(0,3).且点A的坐标为(﹣1,0),点B的坐标为(3,0),点P是抛物线上第一象限内的一个点. 
(1)求抛物线的函数表达式;
(2)连PO、PB,如果把△POB沿OB翻转,所得四边形POP′B恰为菱形,那么在抛物线的对称轴上是否存在点Q,使△QAB与△POB相似?若存在求出点Q的坐标;若不存在,说明理由;
(3)若(2)中点Q存在,指出△QAB与△POB是否位似?若位似,请直接写出其位似中心的坐标.
【答案】
(1)解:∵A(﹣1,0)、B(3,0)、C(0,3)在抛物线y=ax2+bx+c上,
∴ 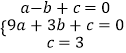 ,
,
解得 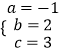 .
.
∴抛物线的解析式为y=﹣x2+2x+3
(2)解:在抛物线的对称轴上存在点Q,使△QAB与△POB相似,如图所示.
∵四边形POP′B为菱形,
∴PO=PB,
∴∠POB=∠PBO.
∵点Q在抛物线的对称轴上,
∴QA=QB,
∴∠QAB=∠QBA.
由△QAB与△POB相似可得∠PBO=∠QBA,
∴点Q、P、B共线.
∵PO=PB,
∴点P在OB的垂直平分线上,
∴xP= ![]() ,
,
此时yP=﹣( ![]() )2+2×
)2+2× ![]() +3=
+3= ![]() ,
,
点P的坐标为( ![]() ,
, ![]() ).
).
设直线PB的解析式为y=mx+n,
则有 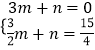 ,
,
解得  .
.
∴直线PB的解析式为y=﹣ ![]() x+
x+ ![]() .
.
∵抛物线的对称轴为x=﹣ ![]() =1,
=1,
∴xQ=1,yQ=﹣ ![]() ×1+
×1+ ![]() =5,
=5,
∴点Q的坐标为(1,5)
根据对称性点Q坐标还可以为(1.﹣5)
(3)解:△QAB与△POB位似,位似中心为点B,点B的坐标为(3,0).

【解析】(1)点A、B、C的坐标已知,只需运用待定系数法就可求出抛物线的解析式;(2)由四边形POP′B为菱形可得PO=PB,从而有∠POB=∠PBO.由点Q在抛物线的对称轴上可得QA=QB,从而有∠QAB=∠QBA.由△QAB与△POB相似可得∠PBO=∠QBA,从而可得点Q、P、B共线.由PO=PB可得点P在OB的垂直平分线上,从而可得xP= ![]() ,代入抛物线即可求出点P的坐标,设直线PB的解析式为y=mx+n,运用待定系数法就可求出直线PB的解析式.由抛物线的对称轴方程可得到点Q的横坐标,代入直线PB的解析式,即可得到点Q的坐标;(3)观察图象,易知△QAB与△POB位似,位似中心即为点B,由此可得到位似中心的坐标.
,代入抛物线即可求出点P的坐标,设直线PB的解析式为y=mx+n,运用待定系数法就可求出直线PB的解析式.由抛物线的对称轴方程可得到点Q的横坐标,代入直线PB的解析式,即可得到点Q的坐标;(3)观察图象,易知△QAB与△POB位似,位似中心即为点B,由此可得到位似中心的坐标.
【考点精析】本题主要考查了确定一次函数的表达式和相似三角形的性质的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;对应角相等,对应边成比例的两个三角形叫做相似三角形才能正确解答此题.

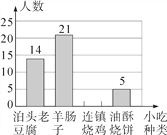
【题目】小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)试验,她们共做了60次试验,试验的结果如下:
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 7 | 9 | 6 | 8 | 20 | 10 |
(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据上述试验,一次试验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次”.小颖和小红的说法正确吗?为什么?