题目内容
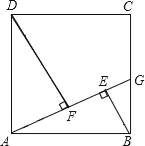
【题目】如图,在边长为4的正方形ABCD中,点G是BC边上的任意一点(不同于端点B、C),连接AG,过B、D两点作BE⊥AG,DF⊥AG,垂足分为E、F.
(1)求证:△ABE≌△DAF;
(2)若△ADF的面积为1,试求|BE﹣DF|的值.
【答案】(1)证明见解析(2)2![]()
【解析】试题分析:
(1)由已知条件易得:∠DFA=∠AEB=∠DAB=90°,从而可得∠ADF+∠DAF=∠DAF+∠BAE=90°,由此即可得到∠ADF=∠BAE,结合正方形ABCD中AD=AB即可证得△ABE≌△DAF;
(2)设AF=a,DF=b,则由△ADF的面积为1可得![]() ,即可得到
,即可得到![]() ;由正方形的边长为4在Rt△ADF中可得:
;由正方形的边长为4在Rt△ADF中可得: ![]() ,由此即可得到
,由此即可得到![]() ,即可解得
,即可解得![]() 的值,从而可由|BE﹣DF|=|AF﹣DF|求出所求的值.
的值,从而可由|BE﹣DF|=|AF﹣DF|求出所求的值.
试题解析:
(1)在正方形ABCD中,∠DAB=90°,AB=AD,
∴∠DAF+∠BAE=90°,
∵DF⊥AG,BE⊥AG,
∴∠AFD=∠BEA=90°,∠DAF+∠ADF=90°,
∴∠BAE=∠ADF,
在△ABE和△DAF中, 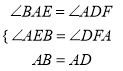 ,
,
∴△ABE≌△DAF(AAS);

(2)∵△ABE≌△DAF,
∴BE=AF,
设AF=a,DF=b,
∵△ADF的面积为1,
∴![]() AFDF=1,即
AFDF=1,即![]() ab=1,
ab=1,
∴ ab=2,
在Rt△ADF中,根据勾股定理得,AF2+DF2=AD2,即a2+b2=42=16,
∴(a﹣b)2=a2﹣2ab+b2=16﹣4=12,
∴|a﹣b|=![]() ,即|AF﹣DF|=|BE﹣DF|=
,即|AF﹣DF|=|BE﹣DF|=![]() .
.

练习册系列答案
相关题目