题目内容
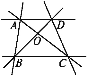
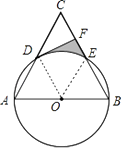
【题目】已知:如图,以等边三角形ABC一边AB为直径的⊙O与边AC、BC分别交于点D、E,过点D作DF⊥BC,垂足为F. 
(1)求证:DF为⊙O的切线;
(2)若等边三角形ABC的边长为4,求DF的长;
(3)写出求图中阴影部分的面积的思路.(不求计算结果)
【答案】
(1)证明:连接OD,如图,
∵△ABC为等边三角形,
∴∠A=∠C=60°,
∵OA=OD,
∴∠ODA=∠A=60°,
∴∠ODA=∠C,
∴OD∥BC,
∵DF⊥BC,
∴OD⊥BC,
∴DF为⊙O的切线
(2)解:∵等边三角形ABC的边长为4,
∴AB=AC=4,∠C=60°,
∵AO=AD=2,
∴CD=2,
在Rt△CDF中,∵sinC= ![]() ,
,
∴DF=2sin60°= ![]()
(3)解:连接OE,如图,
∵CF= ![]() CD=1,
CD=1,
∴EF=CE﹣CF=1,
∴S阴影部分=S梯形ODFE﹣S扇形DOE= ![]() (1+2)
(1+2) ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() π.
π.
【解析】(1)连接OD,如图,利用等边三角形的性质得到∠A=∠C=60°,再证明OD∥BC,然后利用DF⊥BC可得OD⊥BC,再根据切线的判定定理可判断DF为⊙O的切线;(2)利用等边三角形的性质得到AB=AC=4,∠C=60°,则CD=2,然后在Rt△CDF中利用正弦的定义可计算出DF;(3)连接OE,如图,根据扇形的面积公式,利用S阴影部分=S梯形ODFE﹣S扇形DOE进行计算.
【考点精析】掌握等边三角形的性质和切线的判定定理是解答本题的根本,需要知道等边三角形的三个角都相等并且每个角都是60°;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某赛季中国职业篮球联赛第11轮前四名球队积分榜如下:
队名 | 比赛场次 | 胜场 | 负场 | 积分 |
辽宁 | 11 | 11 | 0 | 22 |
北京 | 11 | 10 | 1 | 21 |
广厦 | 11 | 9 | 2 | 20 |
新疆 | 11 | 8 | 3 | 19 |
(1)若一个队胜m场,则总积分为_____;
(2)某队的胜场总积分能否等于它的负场总积分,你的观点是:_____.