Question

【题目】如图，在菱形中，，点，分别在，边上，且，与交于点．若，，则四边形的面积为________．

Answer 1

【答案】

【解析】

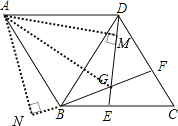
首先利用菱形的性质得出AB=AD，又由AB=BD得出△ABD是等边三角形，进一步证明△CDE≌△DBF，得出∠BGE=∠DGF=60°，证得四边形ABGD是圆内接四边形，过点A再分别作AM⊥DE，AN⊥BF，证明△ABN≌△ADM，把四边形ABGD的面积转化为四边形AMGN的面积即可．

解：∵四边形ABCD是菱形，

∴AB=AD，

又∵AB=BD

∴△ABD是等边三角形，

∴∠BAD=∠ABD=60°

∴∠DBC=∠BDF=∠C=60°

在△CDE和△DBF中，

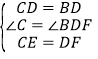
∴△CDE≌△DBF（SAS）

∴∠CDE=∠DBF

∴∠GBE=∠BDE

∴∠DBF+∠GBE=∠DBF+∠BDE=∠BGE=∠DGF=60°=∠BAD

∴四边形ABGD是圆内接四边形，

∴∠BGD=120°

如图，过点A分别作AM⊥DE，AN⊥BF，垂足分别为M、N

∵AG是角平分线，

∴AN=AM，

在Rt△ABN和Rt△ADM中，

,

∴Rt△ABN≌Rt△ADM（HL）

∴BN=DM

∴GN+GM=BG+DG=2+3=5

连接AG，

在Rt△AGN和Rt△AGM中
,

∴Rt△AGN≌Rt△AGM（HL）

∴NG=MG=（BG+DG）=，∠AGN=∠BGD=60°

∴AN=NGtan∠AGN=

∴S四边形ABGD=S四边形ANGM．

S四边形ABGD=2S△AGN，=2××NG×AN=×

=．

故答案为：．