题目内容
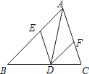
【题目】在△ABC中,∠BAC=90°,以AC为边向外作△ACD,F为BC上一点,连结AF.
(1)如图1,若∠ACD=90°,∠CAD=30°,CD=1,AB=BF=2,求FC的长度.
(2)如图2,若AB=AC,延长DC交AF延长线于H点,且∠AHD=90°,∠BCH=∠CAD,连结BD交AF于M点,求证:CD=2MH.

【答案】(1)CF=![]() ﹣2;(2)见解析
﹣2;(2)见解析
【解析】
(1)先用30°直角三角形的性质求AD的长,进而可求出AC的长,在△ACB中,BC2=AB2+AC2,求出BC的长,则CF=BC﹣BF可求出;
(2)过点B作BN⊥AH,先证明△ABN≌△CAH得AN=CH,BN=AH,根据∠BCH=∠CAD证得△ADH是等腰直角三角形,AH=DH,再证明△BNM≌△DHM得:HM=MN,即CD=2MH.
(1)解:∵∠ACD=90°,∠CAD=30°,CD=1,
∴AD=2,
∴![]() ,
,
在Rt△ABC中,![]() ,
,
∴CF=BC﹣BF=![]() ﹣2.
﹣2.
(2)证明:过点B作BN⊥AH,
∵∠BAC=90°,∠ANB=90°,
∴∠CAH=∠ABN,
在Rt△ABN和Rt△CAH中,
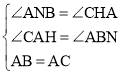 ,
,
∴△ABN≌△CAH(AAS),
∴BN=AH,AN=CH,
∵AB=AC,
∴∠ACB=45°,
∵∠HCA=∠CAD+∠ADH,∠HCA=∠BCH+ACB,∠BCH=∠CAD,
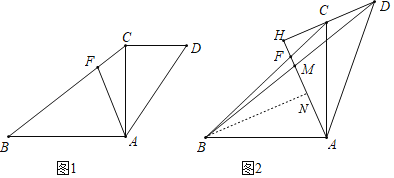
∴∠ADH=∠ACB=45°,
∴AH=DH,
∴BN=DH,
在Rt△BNM和Rt△DHM中,
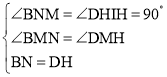 ,
,
∴△BNM≌△DHM(AAS),
∴MH=MN,
∵AH=AN+HN,DH=CH+CD,
∴HN=CD,
∴CD=2MH.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目