题目内容
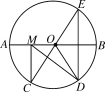
【题目】如图,在⊙O中,AB是⊙O的直径,AB=10,![]() ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=
,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=![]() ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
根据弧AC=弧CD=弧DB和点E是点D关于AB的对称点,求出∠DOB=∠COD=∠BOE=60°,求出∠CED,即可判断①②;根据圆周角定理求出M和A重合时,∠MDE=60°,即可判断③;根据轴对称的性质,求出M的位置,根据圆周角定理求出此时CE为直径,即可得到CE的长,判断④.
∵弧AC=弧CD=弧DB,
∴∠DOB=∠COD=∠BOE=60°,
故①正确;
∵AB为直径,且点E是点D关于AB的对称点
∴∠E=∠D,AB⊥DE
∴∠CED=![]() ∠DOB=30°,
∠DOB=30°,
故②正确;
∵M和A重合时,∠MDE=60°,
∴∠MDE+∠E=90°
∴DM⊥CE
故③不正确;
根据轴对称的性质,可知D与E对称,连接CE,根据两点之间线段最短,可知这时的CM+DM最短,
∵∠DOB=∠COD=∠BOE=60°
∴CE为直径,即CE=10,
故④正确.
故选:C.

练习册系列答案
相关题目