题目内容
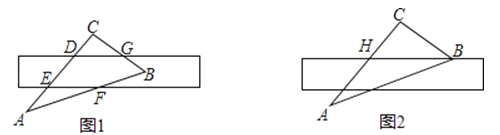
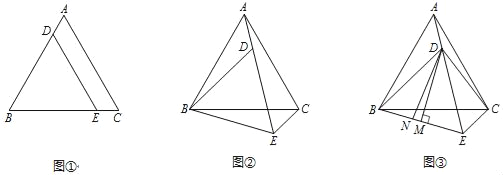
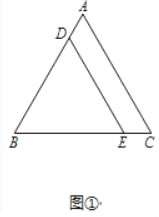
【题目】已知:如图①,△ABC是等边三角形,点D、E分别在边AB、BC上,且BD=BE,连接DE.
(1)求证:DE∥AC;
(2)将图①中的△BDE绕点B顺时针旋转,使得点A、D、E在同一条直线上,如图②,求∠AEC的度数;
(3)在(2)的条件下,如图③,连接CD,过点D作DM⊥BE于点M,在线段BM上取点N,使得∠DNE+∠DCE=180°.求证:EN﹣EC=2MN.
【答案】(1)证明见解析;(2)60°;(3)证明见解析
【解析】
(1)欲证明DE∥AC,只要证明∠DEB=∠C即可;
(2)通过“边角边”证明△ABD≌△CBE,然后推出∠CEB=∠ADB=120°,即可解决问题;
(3)通过“角角边”证明△BDN≌△EDC,得到BN=CE,由DB=DE,DM⊥BE,推出BM=EM,即BN+MN=EN﹣MN,推出CE+MN=EN﹣MN,即EN﹣EC=2MN.
解:(1)证明:如图①中,
∵△ABC是等边三角形,
∴∠B=∠C=60°,
又∵BD=BE,
∴△BDE是等边三角形,
∴∠BED=60°,
∴∠C=∠BED,
∴DE∥AC;
(2)如图2中,

∵△ABC、△BDE都是等边三角形,
∴BA=BC,BD=BE,∠ABC=∠DBE=∠BDE=∠BED=60°,
∴∠ABD=∠CBE,
在△ABD和△CBE中,
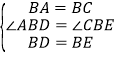 ,
,
∴△ABD≌△CBE(SAS),
∴∠CEB=∠ADB,
∵∠ADB=180°﹣∠BDE=180°﹣60°=120°,
∴∠CEB=120°,
∴∠AEC=∠CEB﹣∠BED=120°﹣60°=60°;
(3)证明:如图3中,

∵∠DNE+∠DCE=180°,∠DNE+∠DNB=180°,
∴∠DCE=∠DNB,
由(1)知△BDE是等边三角形,
∴BD=ED,∠DBE=60°,
由(2)知∠AEC=60°,
∴∠DBE=∠AEC,
在△BDN和△EDC中,
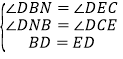 ,
,
∴△BDN≌△EDC(AAS),
∴BN=CE,
∵DB=DE,DM⊥BE,
∴BM=EM,即BN+MN=EN﹣MN,
∴CE+MN=EN﹣MN,
∴EN﹣EC=2MN.