ЬтФПФкШн
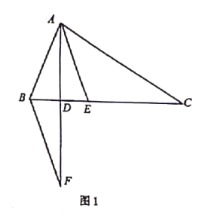
ЁОЬтФПЁПЃЈ1ЃЉШчЭМ1ЃЌдке§ЗНаЮABCDжаЃЌMЪЧBCБпЃЈВЛКЌЖЫЕуBЁЂCЃЉЩЯШЮвтвЛЕуЃЌPЪЧBCбгГЄЯпЩЯвЛЕуЃЌNЪЧЁЯDCPЕФЦНЗжЯпЩЯвЛЕуЃЎШєЁЯAMNЃН90ЁуЃЌЧѓжЄЃКAMЃНMNЃЎ
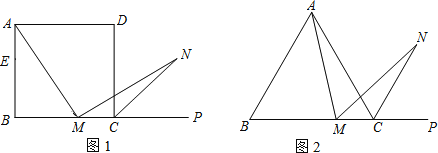
ЯТУцИјГівЛжжжЄУїЕФЫМТЗЃЌФуПЩвдАДетвЛЫМТЗжЄУїЃЌвВПЩвдбЁдёСэЭтЕФЗНЗЈжЄУїЃЎ
жЄУїЃКдкБпABЩЯНиШЁAEЃНMCЃЌСЌНгMEЃЎе§ЗНаЮABCDжаЃЌЁЯBЃНЁЯBCDЃН90ЁуЃЌABЃНBCЃЎЁрЁЯNMCЃН180ЁуЉЁЯAMNЉЁЯAMBЃН180ЁуЉЁЯBЉЁЯAMBЃНЁЯMABЃНЁЯMAEЃЎ
ЃЈЯТУцЧыФуЭъГЩгрЯТЕФжЄУїЙ§ГЬЃЉ
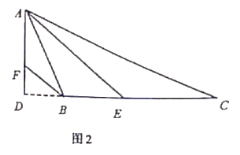
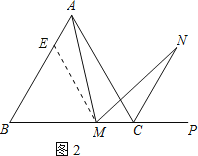
ЃЈ2ЃЉШєНЋЃЈ1ЃЉжаЕФЁАе§ЗНаЮABCDЁБИФЮЊЁАе§Ш§НЧаЮABCЁБЃЈШчЭМ2ЃЉЃЌNЪЧЁЯACPЕФЦНЗжЯпЩЯвЛЕуЃЌдђЁЯAMNЃН60ЁуЪБЃЌНсТлAMЃНMNЪЧЗёЛЙГЩСЂЃПЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉНсТлAMЃНMNЛЙГЩСЂЃЛжЄУїМћНтЮіЃЛ
ЁОНтЮіЁП
ЃЈ1ЃЉдкБпABЩЯНиШЁAEЃНMCЃЌСЌНгMEЃЌгЩЬтжаЬѕМўПЩЕУЁЯAEM=ЁЯMCN=135ЁуЃЌдйгЩСННЧМавЛБпМДПЩХаЖЈШ§НЧаЮШЋЕШЃЛ
ЃЈ2ЃЉЛЙЪЧРћгУСННЧМавЛБпжЄУїЦфШЋЕШЃЌжЄУїЗНЗЈЭЌЃЈ1ЃЉЃЎ
ЃЈ1ЃЉжЄУїЃКдкБпABЩЯНиШЁAEЃНMCЃЌСЌНгMEЃЎ
Ёпе§ЗНаЮABCDжаЃЌЁЯBЃНЁЯBCDЃН90ЁуЃЌABЃНBCЃЎ
ЁрЁЯNMCЃН180ЁуЉЁЯAMNЉЁЯAMBЃН180ЁуЉЁЯBЉЁЯAMBЃНЁЯMABЃНЁЯMAEЃЌ
BEЃНABЉAEЃНBCЉMCЃНBMЃЌ
ЁрЁЯBEMЃН45ЁуЃЌЁрЁЯAEMЃН135ЁуЃЎ
ЁпNЪЧЁЯDCPЕФЦНЗжЯпЩЯвЛЕуЃЌ
ЁрЁЯNCPЃН45ЁуЃЌЁрЁЯMCNЃН135ЁуЃЎ
дкЁїAEMгыЁїMCNжаЃЌЁЯMAEЃНЁЯNMCЃЌAEЃНMCЃЌЁЯAEMЃНЁЯMCNЃЌ
ЁрЁїAEMЁеЁїMCNЃЈASAЃЉЃЌ
ЁрAMЃНMNЃЎ
ЃЈ2ЃЉНтЃКНсТлAMЃНMNЛЙГЩСЂ
жЄУїЃКдкБпABЩЯНиШЁAEЃНMCЃЌСЌНгMEЃЎ
дке§ЁїABCжаЃЌЁЯBЃНЁЯBCAЃН60ЁуЃЌABЃНBCЃЎ
ЁрЁЯNMCЃН180ЁуЉЁЯAMNЉЁЯAMBЃН180ЁуЉЁЯBЉЁЯAMBЃНЁЯMAEЃЌ
BEЃНABЉAEЃНBCЉMCЃНBMЃЌ
ЁрЁЯBEMЃН60ЁуЃЌЁрЁЯAEMЃН120ЁуЃЎ
ЁпNЪЧЁЯACPЕФЦНЗжЯпЩЯвЛЕуЃЌ
ЁрЁЯACNЃН60ЁуЃЌЁрЁЯMCNЃН120ЁуЃЎ
дкЁїAEMгыЁїMCNжаЃЌЁЯMAEЃНЁЯNMCЃЌAEЃНMCЃЌЁЯAEMЃНЁЯMCNЃЌ
ЁрЁїAEMЁеЁїMCNЃЈASAЃЉЃЌ
ЁрAMЃНMNЃЎ

 ПкЫуаФЫуЫйЫугІгУЬтЯЕСаД№АИ
ПкЫуаФЫуЫйЫугІгУЬтЯЕСаД№АИ ЭЌВНЭиеЙдФЖСЯЕСаД№АИ
ЭЌВНЭиеЙдФЖСЯЕСаД№АИЁОЬтФПЁПКьаЧЙЋЫОЩњВњЕФФГжжЪБСюЩЬЦЗУПМўГЩБОЮЊ20дЊЃЌОЙ§ЪаГЁЕїбаЗЂЯжЃЌетжжЩЬЦЗдкЮДРД40ЬьФкЕФ ШеЯњЪлСП(Мў)гыЪБМф(Ьь)ЕФЙиЯЕШчЯТБэЃК
ЪБМф(Ьь) | 1 | 3 | 6 | 10 | 36 | Ё |
ШеЯњЪлСП(Мў) | 94 | 90 | 84 | 76 | 24 | Ё |
ЮДРД40ЬьФкЃЌЧА20ЬьУПЬьЕФМлИёy1(дЊ/Мў)гыtЪБМф(Ьь)ЕФКЏЪ§ЙиЯЕЪНЮЊЃКy1=![]() t+25(1ЁмtЁм20ЧвtЮЊећЪ§)ЃЛКѓ20ЬьУПЬьЕФМлИёy2(д/Мў)гыtЪБМф(Ьь)ЕФКЏЪ§ЙиЯЕЪНЮЊЃКy2=ЁЊ
t+25(1ЁмtЁм20ЧвtЮЊећЪ§)ЃЛКѓ20ЬьУПЬьЕФМлИёy2(д/Мў)гыtЪБМф(Ьь)ЕФКЏЪ§ЙиЯЕЪНЮЊЃКy2=ЁЊ![]() t+40(21ЁмtЁм40ЧвtЮЊећЪ§).ЯТУцЮвУЧРДбаОП етжжЩЬЦЗЕФгаЙиЮЪЬт.
t+40(21ЁмtЁм40ЧвtЮЊећЪ§).ЯТУцЮвУЧРДбаОП етжжЩЬЦЗЕФгаЙиЮЪЬт.
(1)ШЯецЗжЮіЩЯБэжаЕФЪ§СПЙиЯЕЃЌРћгУбЇЙ§ЕФвЛДЮКЏЪ§ЁЂЖўДЮКЏЪ§ ЁЂЗДБШР§КЏЪ§ЕФжЊЪЖШЗЖЈвЛИіТњзуетаЉЪ§ОнжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
(2)ЧыдЄВтЮДРД40ЬьжаФЧвЛЬьЕФЯњЪлРћШѓзюДѓЃЌзюДѓШеЯњЪлРћШѓЪЧЖрЩйЃП
(3)дкЪЕМЪЯњЪлЕФЧА20ЬьжаИУЙЋЫООіЖЈУПЯњЪлвЛМўЩЬЦЗОЭОшдљaдЊРћШѓ(aЃМ4)ИјЯЃЭћЙЄГЬЃЌЙЋЫОЭЈЙ§ЯњЪлМЧТМЗЂЯжЃЌЧА20ЬьжаЃЌУПЬьПлГ§ОшдљКѓЕФШеЯњЪлРћШѓЫцЪБМфtЕФдіДѓЖјдіДѓЃЌЧѓaЕФШЁжЕЗЖЮЇ.
ЁОЬтФПЁПФГЕЅЮЛеаЦИдБЙЄЃЌВЩШЁБЪЪдгыУцЪдЯрНсКЯЕФЗНЪННјааЃЌСНЯюГЩМЈЕФдЪМЗжОљЮЊ![]() Зж.ЧА
Зж.ЧА![]() УћбЁЪжЕФЕУЗжШчЯТЃКИљОнЙцЖЈЃЌБЪЪдГЩМЈКЭУцЪдГЩМЈЗжБ№АДвЛЖЈЕФАйЗжБШелКЯГЩзлКЯГЩМЈЃЈзлКЯГЩМЈЕФТњЗжШдЮЊ
УћбЁЪжЕФЕУЗжШчЯТЃКИљОнЙцЖЈЃЌБЪЪдГЩМЈКЭУцЪдГЩМЈЗжБ№АДвЛЖЈЕФАйЗжБШелКЯГЩзлКЯГЩМЈЃЈзлКЯГЩМЈЕФТњЗжШдЮЊ![]() ЗжЃЉЃЌЯжЕУжЊ
ЗжЃЉЃЌЯжЕУжЊ![]() КХбЁЪжЕФзлКЯГЩМЈЮЊ
КХбЁЪжЕФзлКЯГЩМЈЮЊ![]() Зж.
Зж.
ађКХ |
|
|
|
БЪЪдГЩМЈ/Зж |
|
|
|
УцЪдГЩМЈ/Зж |
|
|
|
ЃЈ1ЃЉЧѓБЪЪдГЩМЈКЭУцЪдГЩМЈИїеМЕФАйЗжБШЃК
ЃЈ2ЃЉЧѓГіЦфгрСНУћбЁЪжЕФзлКЯГЩМЈЃЌВЂвдзлКЯГЩМЈХХађШЗЖЈетШ§УћбЁЪжЕФУћДЮЁЃ