题目内容
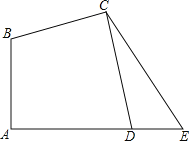
【题目】如图,⊙O的直径AB=4,C是⊙O上一点,连接OC.过点C作CD⊥AB,垂足为D,过点B作BM∥OC,在射线BM上取点E,使BE=BD,连接CE. 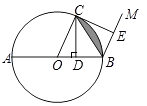
(1)当∠COB=60°时,直接写出阴影部分的面积;
(2)求证:CE是⊙O的切线.
【答案】
(1)解:∵OC=OB,∠COB=60°,
∴△BOC是等边三角形,∴S△BOC= ![]() 22=
22= ![]()
S阴=S扇形OBC﹣S△BOC= ![]() ﹣
﹣ ![]() 22=
22= ![]() ;
;
(2)证明:∵BM∥OC
∴∠OCB=∠CBE.
∵OC=OB
∴∠OCB=∠OBC
∴∠OBC=∠CBE
又BD=BE,BC=BC
△CBD≌△CBE
∴∠CEB=∠CDB=90°.
∵BM∥OC,
∴∠OCE+∠CEB=180°,
∴∠OCE=180°﹣∠CEB=180°﹣90°=90°,
即OC⊥CE,
∴CE是⊙O的切线.
【解析】(1)图中阴影部分的面积=扇形的面积﹣三角形的面积;(2)欲证明CE是⊙O的切线,只需推知∠OCE=90°即可.
【考点精析】掌握切线的判定定理和扇形面积计算公式是解答本题的根本,需要知道切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目