题目内容
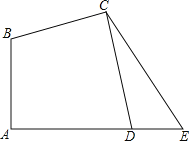
【题目】如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC.延长AD到E点,使DE=AB.连接CE.求∠E的度数.
【答案】45°
【解析】
连接AC,首先根据四边形的内角和等于360°,结合已知条件求出∠ABC+∠ADC=180°,再利用同角的补角相等得到∠ABC=∠CDE,接下来依据“边角边”即可证得△ABC≌△EDC,再利用全等三角形的性质求解即可.
证明:在连接AC.
四边形ABCD中,∵∠BAD=∠BCD=90°,
∴∠ABC+∠ADC=180°,
又∵∠CDE+∠ADC=180°,
∴∠ABC=∠CDE,
在△ABC和△EDC中,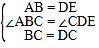 ,
,
∴△ABC≌△EDC(SAS),
∴∠BAC=∠CED,AC=EC,
∴∠EAC=∠CED,∴∠BAC=∠CAE=![]() ∠BAD=
∠BAD=![]() ,
,
∴∠AEC=![]() 即∠E=
即∠E=![]() .
.

练习册系列答案
相关题目