题目内容
【题目】小明同学在做作业时，遇到这样一道几何题：
已知：如图1，l1∥l2∥l3，点A、M、B分别在直线l1，l2，l3上，MC平分∠AMB，∠1=28°，∠2=70°．求：∠CMD的度数．
小明想了许久没有思路，就去请教好朋友小坚，小坚给了他如图2所示的提示：
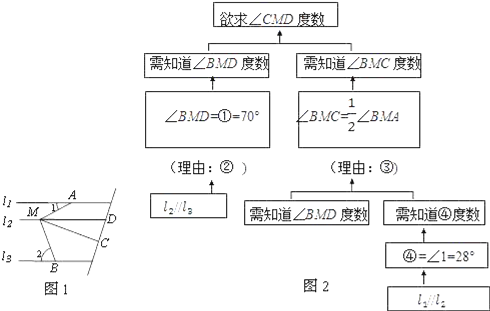
请问小坚的提示中①是∠ ，④是∠ ．
理由②是： ；
理由③是： ；
∠CMD的度数是 °．
【答案】2；AMD；两直线平行，内错角相等；角平分线定义；21
【解析】试题分析：根据两直线平行，内错角相等可得∠BMD=∠2=70°，∠1=∠AMD=28°，即可得∠AMB=∠AMD+∠BMD=98°，根据角平分线的定义可得∠BMC=
∠AMB=49，即可得∠CMD=∠BMD-∠BMC=21°.
试题解析：
∵l1∥l2∥l3，
∴∠1=∠AMD=28°，∠2=∠DMB=70°（两直线平行，内错角相等），
∴∠AMB=28°+70°=98°，
∵MC平分∠AMB，
∴∠BMC=
∠AMB=98°×=49°（角平分线定义），
∴∠DMC=70°﹣49°=21°，
故答案为：2；AMD；两直线平行，内错角相等；角平分线定义；21．
练习册系列答案
名校课堂系列答案
相关题目
