Question

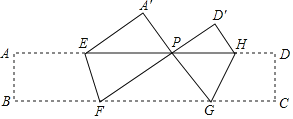
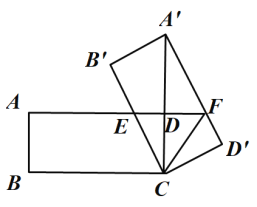
【题目】如图，在矩形ABCD中， AB=3，BC=4，将矩形ABCD绕点C旋转，点A、B、D的对应点分别为A’ 、B’、 D’，当A’ 落在边CD的延长线上时，边A’ D’ 与边 AD的延长线交于点F，联结CF，那么线段CF的长度为____．

Answer 1

【答案】

【解析】

由勾股定理可求A'C=5，可得A'D= A'C-CD=2，由△ECD∽△A'CB'，对应边成比例即可求出DE的长，再由△A'DF∽△CDE求出DF的长，最后在Rt△DFC中由勾股定理即可求出DF.

解：由旋转前后对应边相等可知：A'B'=AB=3，B'C=BC=4

∴由勾股定理可知：A'C=，

∴A'D= A'C-CD=2，

又∠ADC=∠B'=90°，且∠ECD=∠A'CB'，

∴△ECD∽△A'CB'，

∴，代入数据：，

∴，

又A'F∥CE，

∴∠CED=∠A'FD，且∠EDC=∠FDA'，

∴△A'DF∽△CDE，

，代入数据：，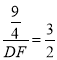

∴，

在Rt△DFC中由勾股定理可知：

.

故答案为：.