题目内容
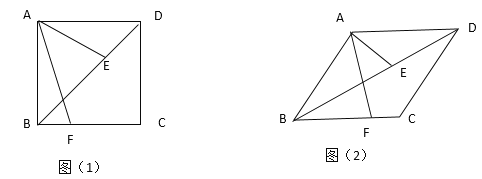
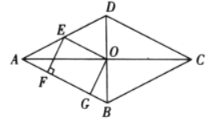
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.
(1)求证:四边形OEFG是矩形;
(2)若AD=10,EF=4,求OE和BG的长.
【答案】(1)见解析;(2)OE=5,BG=2.
【解析】
(1)先证明EO是△DAB的中位线,再结合已知条件OG∥EF,得到四边形OEFG是平行四边形,再由条件EF⊥AB,得到四边形OEFG是矩形;
(2)先求出AE=5,由勾股定理进而得到AF=3,再由中位线定理得到OE=![]() AB=
AB=![]() AD=5,得到FG=5,最后BG=AB-AF-FG=2.
AD=5,得到FG=5,最后BG=AB-AF-FG=2.
解:(1)证明:∵四边形ABCD为菱形,
∴点O为BD的中点,
∵点E为AD中点,
∴OE为△ABD的中位线,
∴OE∥FG,
∵OG∥EF,∴四边形OEFG为平行四边形
∵EF⊥AB,∴平行四边形OEFG为矩形.
(2)∵点E为AD的中点,AD=10,
∴AE=![]()
∵∠EFA=90°,EF=4,
∴在Rt△AEF中,![]() .
.
∵四边形ABCD为菱形,
∴AB=AD=10,
∴OE=![]() AB=5,
AB=5,
∵四边形OEFG为矩形,
∴FG=OE=5,
∴BG=AB-AF-FG=10-3-5=2.
故答案为:OE=5,BG=2.

 特高级教师点拨系列答案
特高级教师点拨系列答案【题目】某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.
设小明计划今年夏季游泳次数为x(x为正整数).
(I)根据题意,填写下表:
游泳次数 | 10 | 15 | 20 | … | x |
方式一的总费用(元) | 150 | 175 | ______ | … | ______ |
方式二的总费用(元) | 90 | 135 | ______ | … | ______ |
(Ⅱ)若小明计划今年夏季游泳的总费用为270元,选择哪种付费方式,他游泳的次数比较多?
(Ⅲ)当x>20时,小明选择哪种付费方式更合算?并说明理由.