题目内容
【题目】在平面直角坐标系xOy中,已知抛物线![]() 与x轴交于点A(3,0)和点B,与y轴相交于点C(0,3),抛物线的顶点为点D.
与x轴交于点A(3,0)和点B,与y轴相交于点C(0,3),抛物线的顶点为点D.
(1)求抛物线的表达式及顶点D的坐标;
(2)联结AD、AC、CD,求∠DAC的正切值;
(3)如果点P是原抛物线上的一点,且∠PAB=∠DAC,将原抛物线向右平移m个单位(m>0),使平移后新抛物线经过点P,求平移距离.
【答案】(1)![]() ,(-1,4); (2)
,(-1,4); (2)![]() ;(3) 平移距离为
;(3) 平移距离为![]() 或
或![]()
【解析】
(1)利用待定系数法构建方程组即可解决问题.
(2)利用勾股定理求出AD,CD,AC,证明∠ACD=90°即可解决问题.
(3)过点P作x轴的垂线,垂足为H.设P(a,-a2-2a+3),可得PH=|-a2-2a+3|,AH=a+3,由∠PAB=∠DAC,推出tan∠PAB=tan∠DAC=![]() .接下来分两种情形,构建方程求解即可.
.接下来分两种情形,构建方程求解即可.
解:(1)抛物线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,
根据题意,得:![]()
解得![]() ,
,![]() .
.
∴抛物线的表达式是![]() ,顶点
,顶点![]() 的坐标为(-1,4);
的坐标为(-1,4);
(2)∵A(-3,0),C(0,3),D(-1,4),
∴![]() ,
,
![]() ,
,
![]() ,
,
∵![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)过点![]() 作
作![]() 轴垂线,垂足为点
轴垂线,垂足为点![]() ,
,
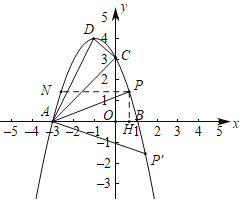
∵点![]() 是抛物线
是抛物线![]() 上一点,
上一点,
∴设![]() ,可得
,可得![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ;
;
(ⅰ)![]() , 解得
, 解得![]() (舍去),
(舍去),![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
过点![]() 作
作![]() 轴平行线与抛物线
轴平行线与抛物线![]() 交于点
交于点![]() ,则点
,则点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,
对称,
由抛物线的对称性可得![]() ,
,
∴平移距离为![]() ;
;
(ⅱ)![]() ,解得
,解得![]() (舍去),
(舍去),![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
过点![]() 作
作![]() 轴平行线与抛物线
轴平行线与抛物线![]() 交于点
交于点![]() ,则点
,则点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,
对称,
由抛物线的对称性可得![]() ,
,
∴平移距离为![]() ,
,
综上所述,平移距离为![]() 或
或![]() .
.

练习册系列答案
相关题目