题目内容
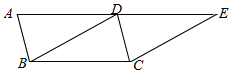
【题目】已知![]() 为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作等边
为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作等边![]() (顶点A、D、E按逆时针方向排列),连接CE.
(顶点A、D、E按逆时针方向排列),连接CE.
(1)问题发现
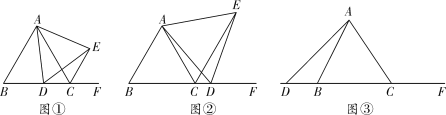
如图①,当点D在边BC上时,填空:
①线段BD,CE之间的数量关系为________;
②线段AC、CE、CD三者之间的数量关系为________;
(2)拓展研究
如图②,当点D在边BC的延长线上且其他条件不变时,请写出AC、CE、CD之间存在的数量关系,并说明理由;
(3)解决问题
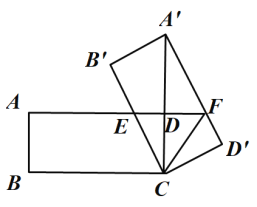
如图③,当点D在边BC的反向延长线上且其他条件不变时,若![]() ,
,![]() ,请直接写出线段CD的长.
,请直接写出线段CD的长.
【答案】(1)①![]() ;②
;②![]() ;(2)
;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]() .
.
【解析】
(1)①观察题图,猜想BD与CE之间的数量关系为相等,在不同三角形中证线段相等首先考虑三角形全等,观察他们分别在![]() 和
和![]() 中,所以证明
中,所以证明![]() 即可;②线段AC、CE、CD之间的数量关系,根据
即可;②线段AC、CE、CD之间的数量关系,根据![]() 得出对应线段的相等关系和等边三角形的性质转化即可得出;(2)同(1)证明;(3)要求CD的长,先找出线段AC、CE、CD之间的数量关系,证法同(1).
得出对应线段的相等关系和等边三角形的性质转化即可得出;(2)同(1)证明;(3)要求CD的长,先找出线段AC、CE、CD之间的数量关系,证法同(1).
(1)①![]() ;
;
②![]() ;
;
【解法提示】①![]() 和
和![]() 都是等边三角形,
都是等边三角形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .在
.在![]() 和
和![]() 中,
中,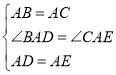 ,
,![]() ,
,![]() ;②
;②![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)AC、CE、CD之间存在的数量关系是:![]() .
.
理由:![]() 和
和![]() 都是等边三角形,
都是等边三角形,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,
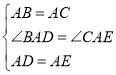 ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(3)![]() .
.
【解法提示】如解图,![]() 和
和![]() 都是等边三角形,
都是等边三角形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .在
.在![]() 和
和![]() 中,
中,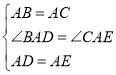 ,
,![]() ,
,![]() .
.![]() ,
,![]() ,
,![]() ,
,![]() .
.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案【题目】某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.
设小明计划今年夏季游泳次数为x(x为正整数).
(I)根据题意,填写下表:
游泳次数 | 10 | 15 | 20 | … | x |
方式一的总费用(元) | 150 | 175 | ______ | … | ______ |
方式二的总费用(元) | 90 | 135 | ______ | … | ______ |
(Ⅱ)若小明计划今年夏季游泳的总费用为270元,选择哪种付费方式,他游泳的次数比较多?
(Ⅲ)当x>20时,小明选择哪种付费方式更合算?并说明理由.