题目内容
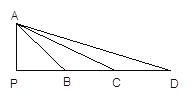
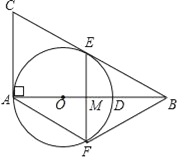
【题目】如图,在Rt△ABC中,∠BAC=90°,O是AB边上的一点,以OA为半径的⊙O与边BC相切于点E.
(1)若AC=6,BC=10,求⊙O的半径.
(2)过点E作弦EF⊥AB于M,连接AF,若∠AFE=2∠ABC,求证:四边形ACEF是菱形.
【答案】(1)圆O半径为r=3;(2)证明见解析.
【解析】试题分析:(1)连接OE,设圆的半径为r,在直角三角形ABC中,利用勾股定理求出AB的长,根据BC与圆相切,得到OE垂直于BC,进而得到一对直角相等,再由一对公共角,利用两角相等的三角形相似得到△BOE与△ABC相似,由相似得比例求出r的值即可;
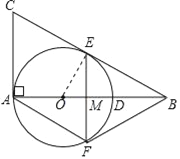
(2)利用同弧所对的圆周角相等,得到∠AOE=4∠B,进而求出∠B与∠F的度数,根据EF与AD垂直,得到一对直角相等,确定出∠MEB=∠F=60°,CA与EF平行,进而得到CB与AF平行,确定出四边形ACEF为平行四边形,再由∠CAB为直角,得到CA为圆的切线,利用切线长定理得到CA=CE,利用邻边相等的平行四边形为菱形即可得证.
试题解析:(1)连接OE,设圆O半径为r,
在Rt△ABC中,AC=6,BC=10,
根据勾股定理得:AB=![]() =8,
=8,
∵BC与圆O相切,∴OE⊥BC,∴∠OEB=∠BAC=90°,
∵∠B=∠B,∴△BOE∽△BCA,∴![]() ,即
,即![]() ,解得:r=3;
,解得:r=3;
(2)∵![]() ,∠AFE=2∠ABC,∴∠AOE=2∠AFE=4∠ABC,
,∠AFE=2∠ABC,∴∠AOE=2∠AFE=4∠ABC,
∵∠AOE=∠OEB+∠ABC,∴∠ABC=30°,∠F=60°,
∵EF⊥AD,∴∠EMB=∠CAB=90°,∴∠MEB=∠F=60°,CA∥EF,∴CB∥AF,
∴四边形ACEF为平行四边形,
∵∠CAB=90°,OA为半径,∴CA为圆O的切线,
∵BC为圆O的切线,∴CA=CE,∴平行四边形ACEF为菱形.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
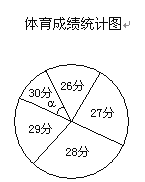
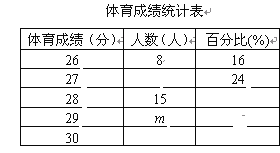
小学生10分钟应用题系列答案【题目】小明在学习了数据的收集、整理与描述后,为妈妈整理记录了10月份的家庭支出情况,并绘制成如下尚不完整的统计图表,请你根据图表信息完成下列各题:
项目 | 物业费 | 伙食费 | 服装费 | 其他费 |
金额/元 | 800 | 400 |
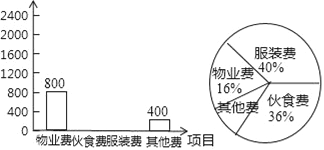
(1)10月份小明家共支出多少元?
(2)在扇形统计图中,表示“其他费”的扇形圆心角为多少度?
(3)请将表格补充完整;
(4)请将条形统计图补充完整.