题目内容
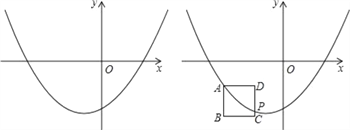
【题目】如图,已知抛物线y=x2﹣2bx﹣3(b为常数,b<0).
发现:(1)抛物线y=x2﹣2bx﹣3总经过一定点,定点坐标为 ;
(2)抛物线的对称轴为直线x= (用含b的代数式表示),位于y轴的 侧.
思考:若点P(﹣2,﹣1)在抛物线y=x2﹣2bx﹣3上,抛物线与反比例函数y=![]() (k>0,x>0)的图象在第一象限内交点的横坐标为a,且满足2<a<3,试确定k的取值范围.
(k>0,x>0)的图象在第一象限内交点的横坐标为a,且满足2<a<3,试确定k的取值范围.
探究:设点A是抛物线上一点,且点A的横坐标为m,以点A为顶点做边长为1的正方形ABCD,AB⊥x轴,点C在点A的右下方,若抛物线与CD边相交于点P(不与D点重合且不在y轴上),点P的纵坐标为﹣3,求b与m之间的函数关系式.
【答案】发现:(1) (0,﹣3);(2)b,左;思考:10<k<36;探究:b=![]() .
.
【解析】试题分析:解:(1)抛物线与y轴的交点为定点;当x=0时,y=x2﹣2bx﹣3=﹣3,
所以抛物线经过定点(0,﹣3);
(2)利用抛物线的对称轴方程得到抛物线的对称轴为直线x=b,然后利用b的范围确定抛物线的对称轴在y轴的左侧;
思考:把P点坐标代入y=x2﹣2bx﹣3得b=﹣1,则抛物线解析式为y=x2+2x﹣3,再分别计算出a=2和a=3所对应的二次函数值,从而确定反比例函数与抛物线的交点的位置,然后利用反比例函数图象上点的坐标特征确定k的范围;
探究:设A(m,m2+2m﹣3),利用正方形的性质得D(m+1,m2+2m﹣3),则P点的坐标为(m+1,﹣3),然后把P(m+1,﹣3)代入y=x2﹣2bx﹣3可得到b与m的关系式.
试题解析:解:(1)当x=0时,y=x2﹣2bx﹣3=﹣3,
所以抛物线经过定点(0,﹣3);
(2)抛物线的对称轴为直线x=﹣![]() =b,
=b,
因为b<0,
所以抛物线的对称轴在y轴的左侧;
故答案为(0,﹣3),b,左;
思考:把P(﹣2,﹣1)代入y=x2﹣2bx﹣3得4+4b﹣3=﹣1,解得b=﹣1,
抛物线解析式为y=x2+2x﹣3,
当a=2时,y=x2+2x﹣3=4+4﹣3=5,
当a=3时,y=x2+2x﹣3=9+6﹣3=12,
所以二次函数图象与反比例函数的交点在抛物线上的点(2,5),(3,12)之间,
所以2×5<k<3×12,
即10<k<36;
探究:设A(m,m2+2m﹣3),
∵正方形ABCD的边长为1,AB⊥x轴,
∴D(m+1,m2+2m﹣3),
∴P点的坐标为(m+1,﹣3),
把P(m+1,﹣3)代入y=x2﹣2bx﹣3得(m+1)2﹣2b(m+1)﹣3=﹣3,
而m+1≠0,
∴m+1﹣2b=0,
∴b=![]() .
.

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案【题目】体育委员统计了全班同学60秒跳绳的次数,并列出下列人数次数分布表,回答下列问题:
次数x | 人数 |
60≤x<80 | 2 |
80≤x<100 | 5 |
100≤x<120 | 21 |
120≤x<140 | 13 |
140≤x<160 | 8 |
160≤x<180 | 4 |
(1)全班有多少人?
(2)组距、组数是多少?
(3)跳绳次数在100≤x<140范围内同学有多少人,占全班的百分之几(精确到0.01%)?