题目内容
【题目】如图,∠APD=90°,AP=PB=BC=CD,则下列结论成立的是( )
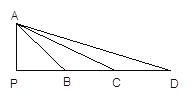
A. ΔPAB∽ΔPDA B. ΔABC∽ΔDCA
C. ΔPAB∽ΔPCA D. ΔABC∽ΔDBA
【答案】D
【解析】根据相似三角形的判定,采用排除法,逐条分析判断.
解:∵∠APD=90°,
而∠PAB≠∠PCB,∠PBA≠∠PAC,
∴无法判定△PAB与△PCA相似,故A错误;
同理,无法判定△PAB与△PDA,△ABC与△DCA相似,故B、D错误;
∵∠APD=90°,AP=PB=BC=CD,
∴AB=![]() PA,AC=
PA,AC=![]() PA,AD=
PA,AD=![]() PA,BD=2PA,
PA,BD=2PA,
∴![]() =
=![]() =
=![]()
![]() =
=![]() =
=![]()
![]() =
=![]() =
=![]()
∴![]() =
=![]() =
=![]()
∴△ABC∽△DBA,故D正确.
故选D.
本题考查相似三角形的判定.识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角,可根据图形提供的数据计算对应角的度数、对应边的比.本题中把若干线段的长度用同一线段来表示是求线段是否成比例时常用的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】体育委员统计了全班同学60秒跳绳的次数,并列出下列人数次数分布表,回答下列问题:
次数x | 人数 |
60≤x<80 | 2 |
80≤x<100 | 5 |
100≤x<120 | 21 |
120≤x<140 | 13 |
140≤x<160 | 8 |
160≤x<180 | 4 |
(1)全班有多少人?
(2)组距、组数是多少?
(3)跳绳次数在100≤x<140范围内同学有多少人,占全班的百分之几(精确到0.01%)?