题目内容
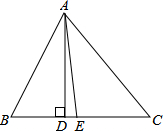
如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平分线,已知∠BAC=82°,∠C=40°,则∠DAE=______.
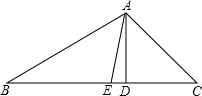

∵∠BAC=82°,∠C=40°,
∴∠B=180°-82°-40°=58°,
∵AE是△ABC的角平分线,
∴∠BAE=
∠BAC=41°,
∵AD是△ABC的高,∴AD⊥BC,∴∠ADB=90°,
在△ABD中,∠BAD=90°-∠B=32°,
∴∠DAE=∠BAE-∠BAD=41°-32°=9°.
∴∠B=180°-82°-40°=58°,
∵AE是△ABC的角平分线,
∴∠BAE=
| 1 |
| 2 |
∵AD是△ABC的高,∴AD⊥BC,∴∠ADB=90°,
在△ABD中,∠BAD=90°-∠B=32°,
∴∠DAE=∠BAE-∠BAD=41°-32°=9°.

练习册系列答案
相关题目