题目内容
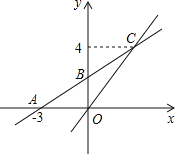
【题目】如图，在平面直角坐标系中，一次函数y=kx+b的图象与x轴交点为A（-3，0），与y轴交点为B，且与正比例函数
的图象的交于点C（m，4）．
（1）求m的值及一次函数y=kx+b的表达式；
（2）若点P是y轴上一点，且△BPC的面积为6，请直接写出点P的坐标．
【答案】（1）m的值为3，一次函数的表达式为
（2） 点P 的坐标为（0， 6）、（0，－2）
【解析】
（1）首先利用待定系数法把C（m，4）代入正比例函数y=
x中，计算出m的值，进而得到C点坐标，再利用待定系数法A、C两点坐标代入一次函数y=kx+b中，计算出k、b的值进而得到一次函数解析式.
（2）利用△BPC的面积为6，即可得出点P的坐标.
解：（1）∵ 点C（m，4）在正比例函数
的图象上，
∴ 
·m， 
即点C坐标为（3，4）
∵ 一次函数 
经过A（－3，0）、点C（3，4）
∴ 
解得：
∴ 一次函数的表达式为
（2） 点P 的坐标为（0， 6）、（0，－2）
“点睛”此题主要考查了待定系数法求一次函数解析式知识，根据待定系数法把A、C两点坐标代入函数y=kx+b中，计算出k、b的值是解题关键.
练习册系列答案
相关题目
