��Ŀ����
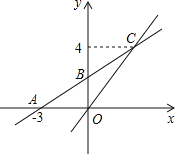
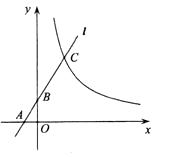
����Ŀ����ͼ����֪������y=m��x+1����x��2����mΪ��������m��0����x������������ν���A��B���㣬��y�ύ�ڵ�C����OA=OC��������B��ֱ���������ߵ���һ����D�ڵڶ����ޣ�
��1���������ߵĺ�������ʽ��
��2������DBA=30�㣬��FΪ�߶�BD��һ�㣨�����˵㣩������AF��һ����M�ӵ�A���������߶�AF��ÿ��1����λ���ٶ��˶���F�������߶�FD��ÿ��2����λ���ٶ��˶���D��ֹͣ������F�������Ƕ���ʱ����M�������˶���������ʱ���٣�
���𰸡�
��1��
�⣺������y=m��x+1����x��2����mΪ��������m��0����x������������ν���A��B���㣬
��y=0�����x=��1��x=2��
��A����1��0����B��2��0����
��OA=OC��
��C��0����1����
�ߵ�C��0����1����������y=m��x+1����x��2���ϣ�
��m����0+1������0��2��=��1��
���m= ![]() ��
��
�������ߵĺ�������ʽΪ��y= ![]() ��x+1����x��2��
��x+1����x��2��
��2��
�⣺�ߡ�DBA=30�㣬
����ֱ��BD�Ľ���ʽΪy=�� ![]() x+b��
x+b��
��B��2��0����
��0=�� ![]() ��2+b�����b=
��2+b�����b= ![]() ��
��
��ֱ��BD�Ľ���ʽΪy=�� ![]() x+
x+ ![]() ��
��
����������ʽ�ɵ� 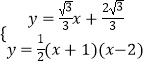 ��
��
��� ![]() ��
�� 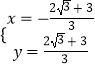 ��
��
��D���� ![]() ��
�� ![]() ����
����
��ͼ������D��DN��x���ڵ�N������D��DK��x�ᣬ
���KDF=��DBA=30�㣮
����F��FG��DK�ڵ�G����FG= ![]() DF��
DF��
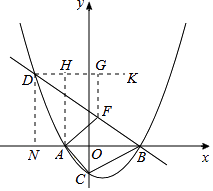
�����⣬����M�˶���·��Ϊ����AF+DF���˶�ʱ�䣺t=AF+ ![]() DF��
DF��
��t=AF+FG�����˶���ʱ��ֵ��������AF+FG�ij���ֵ��
�ɴ��߶���̿�֪������AF+FG�ij��ȵ���СֵΪDK��x��֮��Ĵ��߶Σ�
����A��AH��DK�ڵ�H����t��С=AH��AH��ֱ��BD�Ľ��㣬��Ϊ�����F�㣮
��A�������Ϊ��1��ֱ��BD����ʽΪ��y=�� ![]() x+
x+ ![]() ��
��
��y=�� ![]() ������1��+
������1��+ ![]() =
= ![]() ��
��
��F����1�� ![]() ����
����
��������������F����Ϊ����1�� ![]() ��ʱ����M�������˶���������ʱ����
��ʱ����M�������˶���������ʱ����
����������1�����������A��B���꣬Ȼ�����OA=OC����õ�D���꣬����������y=m��x+1����x��2����mΪ��������m��0������������߽���ʽ����2�������⣬����M�˶���·��Ϊ����AF+DF���˶�ʱ�䣺t=AF+ ![]() DF�����ͼ3���������ߣ���AF+
DF�����ͼ3���������ߣ���AF+ ![]() DFת��ΪAF+FG�����ɴ��߶���̣��õ����߶�AH��ֱ��BD�Ľ��㣬��Ϊ�����F�㣮
DFת��ΪAF+FG�����ɴ��߶���̣��õ����߶�AH��ֱ��BD�Ľ��㣬��Ϊ�����F�㣮
�����㾫����������Ĺؼ�����������κ�����ͼ������֪ʶ�����ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣬�Լ��Զ��κ��������ʵ����⣬�˽������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��

����Ŀ��������������ˮƽ����ߣ������������������Խ��Խ�࣮��Щ���������ȴ��Ϊ��ͨ��ȫ��һ�������������������ijУ��ѧ��ȤС���ڡ��������������ĵ��鱨�桷�о͡�����Ϊ���������������Ч�Ĺ�����ʩ�������ij�������־���������ʾ����飬���е����ʾ���������ѡ�ֻѡһ��� A����ǿ��ͨ����ѧϰ��
B��ʵ�����չ�����
C���Ӵ�ͨΥ���������ȣ�
D�����������������
E����ʱ���·������
�������ݵIJ���ͳ�ƽ�����±���
������ʩ | �ش����� | �ٷֱ� |
A | 25 | 5% |
B | 100 | m |
C | 75 | 15% |
D | n | 35% |
E | 125 | 25% |
�ϼ� | a | 100% |
��1����������ͳ�Ʊ��е����ݿɵ�m= �� n= �� a=��
��2���ڴ���У���ȫ����ͳ��ͼ�� 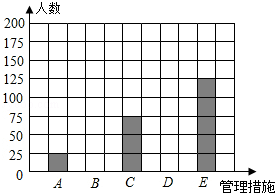
��3���������о���2600�ˣ������������������������ѡ��D������������������ľ���Լ�ж����ˣ�