Question

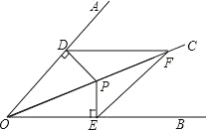
【题目】如图， AC BC ， BD AD ，垂足分别为C 、D ， AC BD ， AC 、BD 交于O

（1）求证： CAB DBA ；

（2）求证： SADO SBCO ．

Answer 1

【答案】（1）详见解析；（2）详见解析.

【解析】

（1）利用“HL”，根据“AB=BA、AC=BD”证Rt△ABC≌Rt△BAD可得；
（2）由Rt△ABC≌Rt△BAD知∠BAC=∠DBA、∠ABC=∠BAD、BC=AD，据此知∠DAO=∠CBO，证△DAO≌△CBO可得．

证明：(1)∵AC⊥BC，BD⊥AD，

∴

在Rt△ABC和Rt△BAD中，

∵

∴Rt△ABC≌Rt△BAD(HL)，

∴∠CAB=∠DBA；

(2)∵Rt△ABC≌Rt△BAD，

∴∠BAC=∠DBA、∠ABC=∠BAD、BC=AD，

∴∠DAO=∠CBO，

在△DAO和△CBO中，

∵

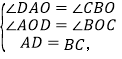
∴△DAO≌△CBO(AAS)，

∴