题目内容
【题目】如图,在□ABCD中,AD是⊙O的弦,BC是⊙O的切线,切点为B.
(1)求证:![]() ;
;
(2)若AB=5,AD=8,求⊙O的半径.
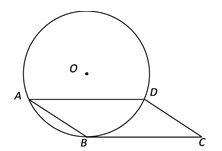
【答案】(1)证明见解析;(2)⊙O的半径为![]()
【解析】
(1) 连接OB,根据题意求证OB⊥AD,利用垂径定理求证;
(2) 根据垂径定理和勾股定理求解.
解:(1)
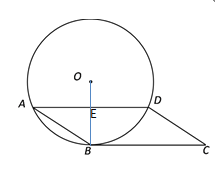
连接OB,交AD于点E.
∵BC是⊙O的切线,切点为B,
∴OB⊥BC.
∴∠OBC=90°
∵ 四边形ABCD是平行四边形
∴AD// BC
∴∠OED=∠OBC =90°
∴ OE⊥AD
又 ∵ OE过圆心O
∴ ![]()
(2)∵ OE⊥AD ,OE过圆心O
∴ AE=![]() AD=4
AD=4
在Rt△ABE中,∠AEB=90°,
BE=![]() =3,
=3,
设⊙O的半径为r,则OE=r-3
在Rt△ABE中,∠OEA=90°,
OE2+AE2 = OA2
即(r-3)2+42= r2 ∴r=![]()
∴⊙O的半径为![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目